

分析 (1)由直方图在得到分数在[50,60)的频率,求出全班人数;由茎叶图求出分数在[80,90)之间的人数,进一步求出概率;
(2)分别算出各段的概率,计算平均分.
解答 解:(1)分数在[50,60)的频率为0.008×10=0.08,由茎叶图知,
分数在[50,60)之间的频数为2,所以全班人数为$\frac{2}{0.08}$=25,
所以分数在[80,90)之间的人数为25-21=4,
则对应的频率为$\frac{4}{25}$=0.16.
所以[80,90)间的小长方形的高为0.16÷10=0.016.
(2)全班共25人,根据各分数段人数得各分数段的频率为:
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频率 | 0.08 | 0.28 | 0.4 | 0.16 | 0.08 |
点评 本题考查了茎叶图和频率分布直方图;关键是正确认识茎叶图和频率分布直方图,从中获取需要的信息.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | $\frac{2}{3}$$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.
如图圆C半径为1,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且$|\overrightarrow{AB}-t\overrightarrow{AC}|≥|\overrightarrow{BC}|$对任意t∈(0,+∞)恒成立,则$\overrightarrow{AB}•\overrightarrow{AC}$=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
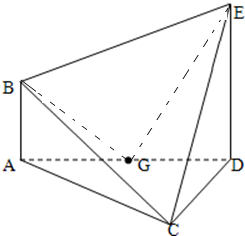 在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.
在如图所示的多面体ABCDE中,AB⊥平面ACD,AB∥DE,AD=DE=2CD=2,四边形ABED的面积为3,∠CAD=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com