
���� ��1��������ɵã�$\left\{\begin{array}{l}{c=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$��������ɵó���
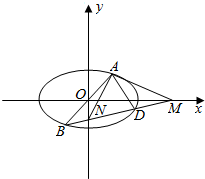
��2����ֱ��AB�ķ���Ϊ��y=kx��A��x1��y1����B��-x1��-y1����D��x2��y2����ֱ��AB�ķ�������Բ�����������A��B�����꣬�ɵ�ֱ��AD�ķ��̣�����Բ���������ɵ�D�����꣬�ɵ�ֱ��BD�ķ��̣�������б�ʼ��㹫ʽ���ɵó���
���  ��1���⣺������ɵã�$\left\{\begin{array}{l}{c=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����c=$\sqrt{2}$��a=$\sqrt{3}$��b=1��
��1���⣺������ɵã�$\left\{\begin{array}{l}{c=\sqrt{2}}\\{\frac{c}{a}=\frac{\sqrt{6}}{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$�����c=$\sqrt{2}$��a=$\sqrt{3}$��b=1��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{3}+{y}^{2}$=1��
��2��֤������ֱ��AB�ķ���Ϊ��y=kx��A��x1��y1����B��-x1��-y1����D��x2��y2����
����$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{3}+{y}^{2}=1}\end{array}\right.$�����A$��\frac{\sqrt{3}}{\sqrt{1+3{k}^{2}}}��\frac{\sqrt{3}k}{\sqrt{1+3{k}^{2}}}��$��B$��\frac{-\sqrt{3}}{\sqrt{1+3{k}^{2}}}��\frac{-\sqrt{3}k}{\sqrt{1+3{k}^{2}}}��$��
��AD��AB����ֱ��AD�ķ���Ϊ��y-$\frac{\sqrt{3}k}{\sqrt{1+3{k}^{2}}}$=$-\frac{1}{k}$$��x-\frac{\sqrt{3}k}{\sqrt{1+3{k}^{2}}}��$��
��Ϊy=-$\frac{1}{k}$x+$\frac{\sqrt{3}��1+{k}^{2}��}{k\sqrt{1+3{k}^{2}}}$��
������Բ���̿ɵã�$\frac{{x}^{2}}{3}$+$[-\frac{1}{k}x+\frac{\sqrt{3}��1+{k}^{2}��}{k\sqrt{1+3{k}^{2}}}]^{2}$=1��
����$\sqrt{1+3{k}^{2}}��{k}^{2}+3��{x}^{2}$-$6\sqrt{3}$��1+k2��x+$\frac{3��5{k}^{2}+3��}{\sqrt{1+3{k}^{2}}}$=0��
���x1=$\frac{\sqrt{3}}{\sqrt{1+3{k}^{2}}}$��x2=$\frac{\sqrt{3}��5{k}^{2}+3��}{��{k}^{2}+3��\sqrt{1+3{k}^{2}}}$��
y1=$\frac{\sqrt{3}k}{\sqrt{1+3{k}^{2}}}$��
y2=$\frac{\sqrt{3}k��{k}^{2}-1��}{��{k}^{2}+3��\sqrt{1+3{k}^{2}}}$��
��kBD=$\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}}$=$\frac{k}{3}$=k1��
BD�ķ���Ϊ��y+$\frac{\sqrt{3}k}{\sqrt{1+3{k}^{2}}}$=$\frac{k}{3}$$��x+\frac{\sqrt{3}}{\sqrt{1+3{k}^{2}}}��$��
��y=0�����xM=$\frac{2\sqrt{3}}{\sqrt{1+3{k}^{2}}}$����M$��\frac{2\sqrt{3}}{\sqrt{1+3{k}^{2}}}��0��$��
��k2=$\frac{{y}_{1}}{{x}_{1}-{x}_{M}}$=-k��
��3k1=-k2��
���=-$\frac{1}{3}$��
���� ���⿼������Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢б�ʼ��㹫ʽ�����ֱ��б��֮��Ĺ�ϵ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+4y+4=0 | B�� | x-4y-4=0 | C�� | x-4y+4=0 | D�� | x+4y-4=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
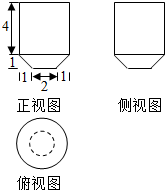
| A�� | $\frac{53}{3}$�� | B�� | $\frac{55}{3}$�� | C�� | 18�� | D�� | $\frac{76}{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
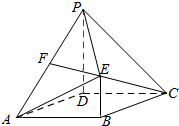 ��ͼ���ı���ABCD�����Σ�PD��ƽ��ABCD��PD��BE��AD=PD=2BE=2����DAB=60�㣬��FΪPA���е㣮
��ͼ���ı���ABCD�����Σ�PD��ƽ��ABCD��PD��BE��AD=PD=2BE=2����DAB=60�㣬��FΪPA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
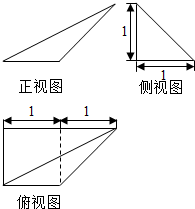
| A�� | 1 | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{5}}{2}$ | D�� | $\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
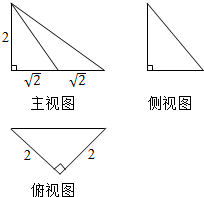
| A�� | 4$\sqrt{3}$�� | B�� | 12�� | C�� | 24�� | D�� | 48�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com