
如图,四棱锥 中,底面
中,底面 是矩形,
是矩形, 底面
底面 ,
, ,点
,点 是侧棱
是侧棱 的中点.
的中点.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)若 ,求二面角
,求二面角 的余弦值.
的余弦值.

(1)见解析;(2)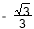
【解析】试题分析:(1)利用直线垂直于平面内两条相交直线,证明线面垂直;(2)建立空间直角坐标系,利用平面的法向量求二面角的余弦值,注意:所求二面角是钝角.
试题解析:(Ⅰ)由于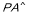 底面
底面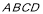
∴面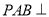 面
面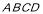
∵面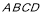 是矩形
是矩形
∴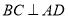
∴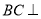 面
面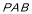
∴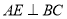
而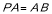 ,
,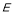 是
是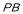 的中点
的中点
∴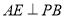
∴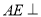 面
面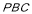
(Ⅱ)分别以 、
、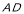 、
、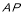 所在直线为
所在直线为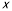 轴、
轴、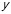 轴、
轴、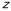 轴建立如图所示的直角坐标系
轴建立如图所示的直角坐标系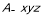 ,
,

则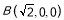 、
、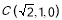 、
、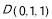 、
、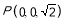
∴
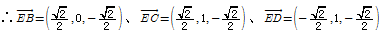
解法一:由(1)可知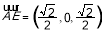 是平面EBC的一个法向量
是平面EBC的一个法向量
设平面ECD的一个法向量为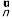 =(x,y,z)
=(x,y,z)
由 ,
,
得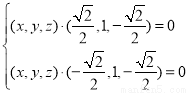
即 ,
,
可得
取y=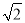 ,得z=2
,得z=2
即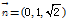
解法二: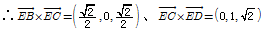
可取平面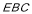 和平面
和平面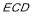 的法向量分别是
的法向量分别是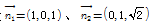
而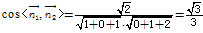
结合图形可知:二面角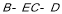 是钝角,故余弦值是
是钝角,故余弦值是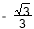
解法三:由已知BC=BE=AD=AE=1,故CD=DE=AB=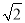
即△CBE和△CDE都是等腰三角形
取CE中点F,连结BD、BF、DF,
有BF⊥CE,DF⊥CE,即∠BFD为二面角B-CE-D的平面角


则BD=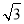 ,BF=
,BF=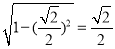 ,DF=
,DF=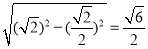
于是cos∠BFD=
故二面角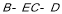 的余弦值是
的余弦值是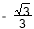
考点:空间直线与平面垂直,二面角,空间向量


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届四川省成都市高新区高三9月月考理科数学试卷(解析版) 题型:选择题
将函数 的图象向左平移
的图象向左平移 个单位长度,所得图象对应的函数( )
个单位长度,所得图象对应的函数( )
(A)在区间 上单调递减 (B)在区间
上单调递减 (B)在区间 上单调递增
上单调递增
(C)在区间 上单调递减 (D)在区间
上单调递减 (D)在区间 上单调递增
上单调递增
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市毕业班摸底测试理科数学试卷(解析版) 题型:选择题
已知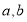 是两条不同的直线,
是两条不同的直线,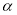 是一个平面,则下列说法正确的是( )
是一个平面,则下列说法正确的是( )
A、若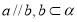 ,则
,则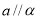 B、若
B、若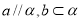 ,则
,则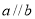
C、若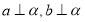 ,则
,则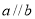 D、若
D、若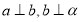 ,则
,则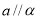
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市毕业班摸底测试文科数学试卷(解析版) 题型:选择题
已知双曲线 (a>0,b>0)的一条渐近线与圆
(a>0,b>0)的一条渐近线与圆 相交于A,B两点,若|AB|=2,则该双曲线的离心率为( )
相交于A,B两点,若|AB|=2,则该双曲线的离心率为( )
A、8 B、2 C、3 D、
C、3 D、
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市毕业班摸底测试文科数学试卷(解析版) 题型:选择题
设全集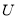 ={1,2,3,4},集合
={1,2,3,4},集合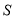 ={1,3},
={1,3},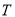 ={4},则
={4},则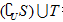 等于( )
等于( )
A、{2,4} B、{4} C、Φ D、{1,3,4}
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三九月月考理科数学试卷(解析版) 题型:选择题
“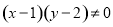 ”是“
”是“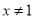 或
或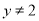 ”成立的( )
”成立的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三九月月考文科数学试卷(解析版) 题型:选择题
定义区间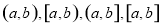 的长度均为
的长度均为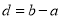 .用
.用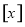 表示不超过x的最大整数.记
表示不超过x的最大整数.记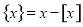 ,其中
,其中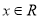 .设
.设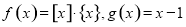 ,若用d表示不等式
,若用d表示不等式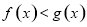 解集区间的长度,则当
解集区间的长度,则当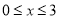 时,有( )
时,有( )
A.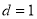 B.
B.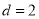 C.
C.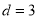 D.
D.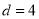
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com