（本小题满分12分）等差数列{an}满足:a1=1， a2+a6=14；正项等比数列{bn}满足:b1=2，b3 =8．
（1）求数列{an}，{bn}的通项公式an，bn；
（2）求数列{an·bn}的前n项和Tn．
激活思维优加课堂系列答案
活力试卷系列答案科目：高中数学 来源：2014-2015学年甘肃省高一下学期期中考试数学试卷（解析版） 题型：选择题
设扇形的周长为8
，面积为4
，则扇形的圆心角是（ ）rad
A．1 B．2 C．
D．1或2
查看答案和解析>>
科目：高中数学 来源：2015-2016学年湖北宜昌市高一上期中考试数学试卷（解析版） 题型：解答题
（本题满分12分）已知幂函数
在
上单调递增，函数
．
（1）求
的值；
（2）当
时，记
、
的值域分别为集合
、
，若
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年河北衡水冀州中学高二上期中理科数学B卷（解析版） 题型：解答题
（本小题12分）某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成六组后，得到频率分布直方图（如图），观察图形中的信息，回答下列问题．
（1）从频率分布直方图中，估计本次考试成绩的中位数；
（2）若从第1组和第6组两组学生中，随机抽取2人，求所抽取2人成绩之差的绝对值大于10的概率．
查看答案和解析>>
科目：高中数学 来源：2016届四川省巴中市普通高中高三10月零诊考试理科数学试卷（解析版） 题型：解答题
（本小题满分12分）已知函数
在x=1处的切线方程为x-y=1．
（1）求f（x）的表达式；
（2）若f（x）≥g（x）恒成立，则称f（x）为g（x）的一个“上界函数”，当（1）中的函数f（x）为函数g（x）=
lnx（t∈R）的一个上界函数时，求实数t的取值范围；
（3）当m>0时，对于（1）中的f（x），讨论F（x）= f（x）+
在区间（0，2）上极值点的个数．
查看答案和解析>>
科目：高中数学 来源：2015-2016学年四川省高二10月月考数学试卷（解析版） 题型：选择题
如图是正方体的平面展开图．在这个正方体中，①BM与ED平行；②CN与BE是异面直线；③CN与BM成60°角；④DM与BN垂直．
以上四个命题中，正确的命题序号是（ ）
A．①②③ B．③④ C．②④ D．②③④
查看答案和解析>>
科目：高中数学 来源：2016届广东省惠州市高三上学期第二次调研考试文科数学试卷（解析版） 题型：解答题
（本小题满分12分）已知数列{
}的前n项和为
，且满足
．
（Ⅰ）证明：数列
为等比数列，并求数列{
}的通项公式；
（Ⅱ）数列{
}满足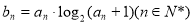
，其前n项和为
，试求满足
的最小正整数n．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的各项均为正数，且
，则
__________．
，
，若
，那么
的夹角等于____________.