
设椭圆E中心在原点,焦点在x轴上,短轴长为4,点Q(2,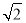 )在椭圆上.
)在椭圆上.
(1)求椭圆E的方程;
(2)设动直线L交椭圆E于A、B两点,且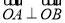 ,求△OAB的面积的取值范围.
,求△OAB的面积的取值范围.
(3)过M(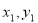 )的直线
)的直线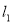 :
: 与过N(
与过N( )的直线
)的直线 :
: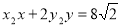 的交点P(
的交点P(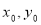 )在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求
)在椭圆E上,直线MN与椭圆E的两准线分别交于G,H两点,求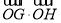 的值.
的值.
(1)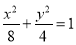 ;(2)
;(2)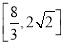 ;(3)-8.
;(3)-8.
【解析】试题分析:(1)由已知b=2,再由点Q在曲线上,可求得a的值;(2)设直线方程为y=kx+m,根据 ,可得k与m的关系,然后用m和k表示出三角形面积,利用均值定理可求其范围,注意不要漏掉斜率不存在的情况;(3)利用l1、l2的交点找出x0,y0的关系,然后将表示为x0,y0的表达式求值。
,可得k与m的关系,然后用m和k表示出三角形面积,利用均值定理可求其范围,注意不要漏掉斜率不存在的情况;(3)利用l1、l2的交点找出x0,y0的关系,然后将表示为x0,y0的表达式求值。
试题解析:(1)因为椭圆E: 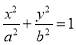 (a>b>0)过M(2,
(a>b>0)过M(2, ) ,2b=4
) ,2b=4
故可求得b=2,a=2
椭圆E的方程为 3分
3分
(2)设P(x,y),A(x1,y1),B(x2,y2),当直线L斜率存在时设方程为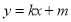 ,
,
解方程组 得
得 ,即
,即 ,
,
则△=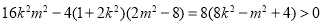 ,
,
即 (*)
(*)
 ,
,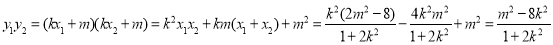
要使 ,需使
,需使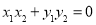 ,即
,即 ,
,
所以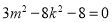 , 即
, 即 ①
①
将它代入(*)式可得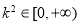
P到L的距离为
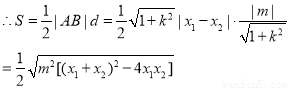
将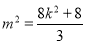 及韦达定理代入可得
及韦达定理代入可得
当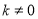 时
时
由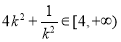 故
故
当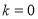 时,
时, 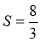
当AB的斜率不存在时,  ,综上S
,综上S 8分
8分
(3)点P(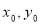 )在直线
)在直线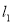 :
: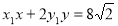 和
和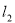 :
: 上,
上,
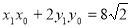 ,
,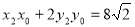
故点M(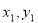 )N(
)N(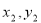 )在直线
)在直线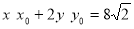 上
上
故直线MN的方程,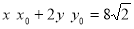 上
上
设G,H分别是直线MN与椭圆准线, 的交点
的交点
由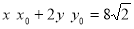 和
和 得G(-4,
得G(-4,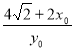 )
)
由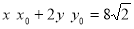 和
和 得H(4,
得H(4,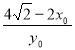 )
)
故

 =-16+
=-16+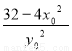
又P(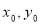 )在椭圆E:
)在椭圆E: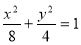
有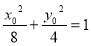 故
故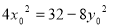


 =-16+
=-16+ =-8 13分
=-8 13分
考点:椭圆的标准方程,直线与椭圆的位置关系,平面向量


科目:高中数学 来源: 题型:
|
| 8cosθ |
| 1-cos2θ |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:选择题
设p:(x-2)(y-5)≠0;q:x≠2或y≠5;r:x+y≠7;则下列命题:
①p是r的既不充分也不必要条件;②p是q的充分不必要条件;③q是r的必要不充分条件.
其中全部真命题有( )
A. ①② B. ①③ C. ②③ D.①②③
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考理科数学试卷(解析版) 题型:选择题
设曲线y=ax―ln(x+1)在点(0,0)处的切线方程为y=2x,则a= ( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:填空题
在棱长为1的正方体ABCD﹣A1B1C1D1中,点M和N分别是矩形ABCD和BB1C1C的中心,则过点A、M、N的平面截正方体的截面面积为 _________ .
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市高三10月考文科数学试卷(解析版) 题型:选择题
已知三个数2,m,8构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A.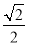 B.
B.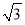 C.
C.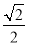 或
或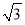 D.
D.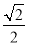 或
或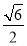
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:填空题
若数列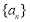 满足:存在正整数
满足:存在正整数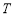 ,对于任意正整数
,对于任意正整数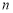 都有
都有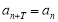 成立,则称数列
成立,则称数列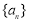 为周期数列,周期为
为周期数列,周期为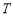 . 已知数列
. 已知数列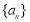 满足
满足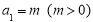 ,
, 现给出以下命题:
现给出以下命题:
①若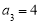 ,则
,则 可以取3个不同的值
可以取3个不同的值
②若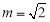 ,则数列
,则数列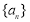 是周期为
是周期为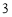 的数列
的数列
③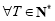 且
且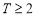 ,存在
,存在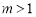 ,
, 是周期为
是周期为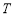 的数列
的数列
④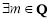 且
且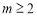 ,数列
,数列 是周期数列.其中所有真命题的序号是 .
是周期数列.其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都实验外国语高三11月月考理科数学试卷(解析版) 题型:选择题
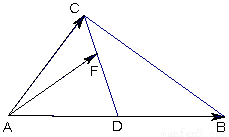
如图所示,在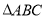 中,
中,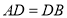 ,
,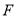 在线段
在线段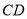 上,设
上,设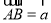 ,
,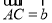 ,
,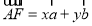 ,则
,则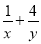 的最小值为( )
的最小值为( )
A.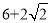 B. 9
B. 9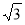 C. 9 D.
C. 9 D. 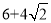
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com