
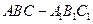 中,
中, .
. 
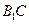 ∥平面
∥平面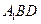 ;
; .
.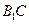 ∥平面
∥平面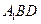 ,证明略。
,证明略。 ,证明略。
,证明略。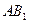 ,
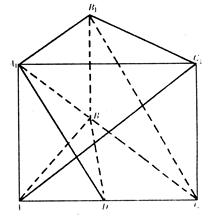
,
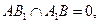 ………………………………………………………………1分
………………………………………………………………1分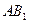 中点,……………………………………………………………………………2分
中点,……………………………………………………………………………2分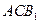 中,有OD∥
中,有OD∥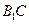 .………………………………………………………………3分
.………………………………………………………………3分 平面
平面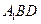 ,……………………………………4分
,……………………………………4分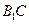
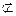 平面
平面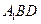 ,……………………………………5分
,……………………………………5分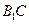 ∥平面
∥平面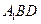 .……………………………………6分
.……………………………………6分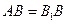 ,
,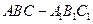 为直三棱柱,
为直三棱柱,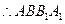 为正方形,
为正方形, …………………………………………7分
…………………………………………7分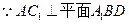 ,
, ,
,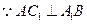 ,………………………………………8分
,………………………………………8分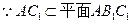 ,
,

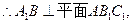
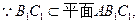
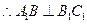 .……………………………………………………………………9分
.……………………………………………………………………9分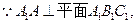

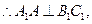 ……………………………………………………………………10分
……………………………………………………………………10分
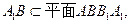
 ………………………………………………………………11分
………………………………………………………………11分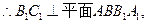 ……………………………………………………………12分
……………………………………………………………12分

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:不详 题型:解答题
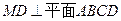 ,
, 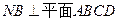 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由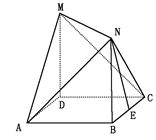
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
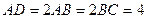 ,
,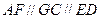 且
且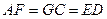 ,
, ,
,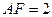 ,H是棱EF的中点
,H是棱EF的中点







 (1)证明:平面
(1)证明:平面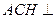 平面CDE;
平面CDE;
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
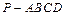 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.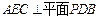 ;
; 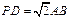 且E为PB的中点时,
且E为PB的中点时,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
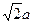 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.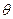 的大小.
的大小. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com