
分析 先化简集合P={-3,2},集合S中至多有一个元素,分类对其求解即可,本题要分成两类,一类为元解,一类为有一解.
解答 解:集合P={-3,2},集合S中至多有一个元素,
若集合S为空集,即a=0时,显然满足条件S⊆P,故a=0.
若集合S非空集,即a≠0,此时S={-$\frac{1}{a}$},若-$\frac{1}{a}$=-3,则a=$\frac{1}{3}$,若-$\frac{1}{a}$=2,则a=-$\frac{1}{2}$
故由a的可取值组合的集合为{0,$\frac{1}{3}$,-$\frac{1}{2}$}.
点评 本题的考点是集合的包含关系判断及应用,本题考查利用集合的包含关系求参数,此类题一般要进行分类讨论求参数的值,求解本题时不要忘记集合为空集的情况,此为本题的易错点.


 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2014}{2015}$ | B. | $\frac{2011}{2012}$ | C. | $\frac{2012}{2013}$ | D. | $\frac{2013}{2014}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{10}{69}$ | C. | $\frac{1}{4}$ | D. | $\frac{10}{39}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
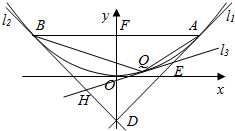 如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.
如图,已知抛物线C:x2=2py(p>0),其焦点F到准线的距离为2,点A、点B是抛物线C上的定点,它们到焦点F的距离均为2,且点A位于第一象限.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com