
【题目】推进垃圾分类处理,是落实绿色发展理念的必然选择,也是打赢污染防治攻坚战的重要环节.为了解居民对垃圾分类的了解程度,某社区居委会随机抽取1000名社区居民参与问卷测试,并将问卷得分绘制频率分布表如表:
得分 |
|
|
|
|
|
|
|
男性 人数 | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性 人数 | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率;
(2)将居民对垃圾分类的了解程度分为“比较了解”(得分不低于60分)和“不太了解”(得分低于60分)两类,完成2×2列联表,并判断是否有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关?
不太了解 | 比较了解 | 合计 | |
男性 | |||
女性 | |||
合计 |
(3)从参与问卷测试且得分不低于80分的居民中,按照性别进行分层抽样,共抽取10人,现从这10人中随机抽取3人作为环保宣传队长,设3人中男性队长的人数为ξ,求ξ的分布列和期望.
附:![]()
![]() ,(n=a+b+c+d).
,(n=a+b+c+d).
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】(1)![]() ;(2)列联表见解析,有把握;(3)分布列见解析,
;(2)列联表见解析,有把握;(3)分布列见解析,![]() .
.
【解析】
(1)用得分不低于60分的频数除以样本容量可得答案;
(2)根据频率分布表可得2×2列联表,计算![]() ,结合临界值表可得结论;
,结合临界值表可得结论;
(3)根据分层抽样可知,男性抽6人,女性抽4人,所以ξ的可能取值有0,1,2,3,再根据古典概型的概率公式计算ξ的各个取值的概率即可得分布列,再用期望公式可得期望.
(1)小区1000名居民中,得分不低于60分的人数为:130+110+60+30+110+100+40+20=600,
故从该社区随机抽取一名居民参与问卷测试,试估计其得分不低于60分的概率为P![]() .
.
(2)2×2列联表如下:
不太了解 | 比较了解 | 合计 | |
男性 | 250 | 330 | 580 |
女性 | 150 | 270 | 420 |
合计 | 400 | 600 | 1000 |
![]()
![]()
![]() 5.54,
5.54,
∵5.54>3.841,
∴有95%的把握认为“居民对垃圾分类的了解程度”与“性别”有关.
(3)参与问卷测试且得分不低于80分的居民中,男性有90人,女性有60人,
若按分层抽样的办法从中抽取10人,则男性人数为10![]() 6,女性人数为10
6,女性人数为10![]() 4.
4.
故ξ的可能取值有0,1,2,3.
P(ξ=0)![]() ,P(ξ=1)
,P(ξ=1)![]() ,P(ξ=2)
,P(ξ=2)![]() ,P(ξ=3)
,P(ξ=3)![]() .
.
∴ξ的分布列为:
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
E(ξ)=0![]() 1
1![]() 2
2![]() 3
3![]()
![]() .
.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是一个给定的非零实数,在平面直角坐标系
是一个给定的非零实数,在平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() 且
且![]() ,点
,点![]() .
.
(1)设![]() 是
是![]() 上的任意一点,试求线段
上的任意一点,试求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程并指出曲线
的方程并指出曲线![]() 的类型和位置;
的类型和位置;
(2)求出![]() 、
、![]() 在它们的交点
在它们的交点![]() 处的各自切线之间的夹角
处的各自切线之间的夹角![]() (锐角)(用反三角函数式表示)
(锐角)(用反三角函数式表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 上的一点,若
上的一点,若![]() 平面
平面![]() ,
,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() ,
,![]() .
.
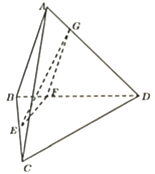
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.将一组数据中的每个数据都乘以同一个非零常数a后,方差也变为原来的a倍
B.设有一个回归方程![]() ,变量x增加1个单位时,y平均减少5个单位
,变量x增加1个单位时,y平均减少5个单位
C.线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱
D.在某项测量中,测量结果ξ服从正态分布N(1,σ2)(σ>0),则P(ξ>1)=0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆![]() 的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附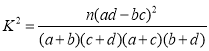 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com