
分析 (1)求出函数的导数,计算f′(-1),f(-1),得到关于a的方程,解出即可;
(2)求出F(x)的表达式,求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极大值即可.
解答 解:(1)∵f(x)=-x3+ax2-4,
∴f′(x)=-3x2+2ax,
f′(-1)=-3-2a,f(-1)=a-3,
∵f(-1)+f′(-1)=-8,
∴a-3-3-2a=-8,解得:a=2,
∴f(a)=f(2)=-4;
(2)由(1)得:a=2,
∴f(x)=-x3+2x2-4,f′(x)=-3x2+4x,
∴F(x)=-x3-x2-4,
F′(x)=-3x2-2x=-x(3x+2),
令F′(x)>0,解得:-$\frac{2}{3}$<x<0,
令F′(x)<0,解得:x>0或x<-$\frac{2}{3}$,
∴F(x)在(-∞,-$\frac{2}{3}$)递减,在(-$\frac{2}{3}$,0)递增,在(0,+∞)递减,
∴F(x)极大值=F(0)=-4.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:解答题
设等差数列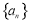 的前
的前 项和为
项和为 .且
.且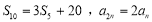 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令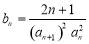 ,数列
,数列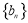 的前
的前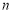 项和
项和 ,证明:对任意
,证明:对任意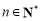 ,都有
,都有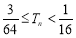 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1)∪(1,$\sqrt{3}$) | B. | (-1,1) | C. | (-$\sqrt{3}$,$\sqrt{3}$) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3,4,5} | B. | {-2,-1,0,1} | ||
| C. | {-5,-4,-3,-2,-1,0,1} | D. | {-5,-4,-3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com