
分析 (1)以-x代替x,建立方程,与已知方程联立,即可求函数f(x)和g(x)的解析式;
(2)由题,即存在${x_0}∈[\frac{1}{2},1]$,$a=-\frac{{g(2{x_0})}}{{f({x_0})}}$,构造函数,确定其范围,即可求实数a的取值范围.
解答 解:(1)由$f(x)+g(x)={(\frac{1}{2})^x}$得$f(-x)+g(-x)={(\frac{1}{2})^{-x}}$,即$-f(x)+g(x)={(\frac{1}{2})^{-x}}$,
所以$f(x)=\frac{1}{2}({2^{-x}}-{2^x})$,$g(x)=\frac{1}{2}({2^{-x}}+{2^x})$.
(2)由题,即存在${x_0}∈[\frac{1}{2},1]$,$a=-\frac{{g(2{x_0})}}{{f({x_0})}}$,
设$h(x)=-\frac{g(2x)}{f(x)}$,则h(x)=$-\frac{{\frac{1}{2}({2^{-2x}}+{2^{2x}})}}{{\frac{1}{2}({2^{-x}}-{2^x})}}$=$\frac{{{2^{2x}}+{2^{-2x}}}}{{{2^x}-{2^{-x}}}}$=$({2^x}-{2^{-x}})+\frac{2}{{{2^x}-{2^{-x}}}}$,
$x∈[\frac{1}{2},1]$时,${2^x}-{2^{-x}}∈[\frac{{\sqrt{2}}}{2},\frac{3}{2}]$,
设t=2x-2-x,则$t∈[\frac{{\sqrt{2}}}{2},\frac{3}{2}]$,而$h(x)=t+\frac{2}{t}$,$y=t+\frac{2}{t}$在$[\frac{{\sqrt{2}}}{2},\sqrt{2}]$是递减,在$[\sqrt{2},\frac{3}{2}]$上递增,
因此${y_{最小}}=\sqrt{2}+\frac{2}{{\sqrt{2}}}=2\sqrt{2}$,${y_{最大}}=\frac{{\sqrt{2}}}{2}+\frac{2}{{\frac{{\sqrt{2}}}{2}}}=\frac{{5\sqrt{2}}}{2}$,
所以$h(x)∈[2\sqrt{2},\frac{{5\sqrt{2}}}{2}]$,即$a∈[2\sqrt{2},\frac{{5\sqrt{2}}}{2}]$.
点评 本题考查函数的奇偶性,考查函数的最值,正确构造函数是关键.


科目:高中数学 来源: 题型:选择题
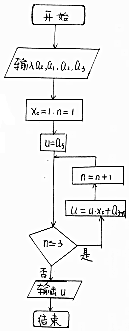 如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )
如图程序框图的算法思路来源于我国古代数学名著《数学九章》中的“秦九韶算法”求多项式的值.执行程序框图,若输入a0=1,a1=1,a2=0,a3=-1,则输出的u的值为( )| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lnx0 | B. | $ln\sqrt{x_0}$ | C. | ln(lnx0) | D. | ${(ln{x_0})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-2 | B. | $y=\frac{{{x^2}-4}}{x+2}$ | C. | $y=\frac{{{{({x-2})}^2}}}{x-2}$ | D. | $y={({\frac{x-2}{{\sqrt{x-2}}}})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com