
���� ������������ĵ��������ݵ����ļ������弴��������߷��̣�
������������ĵ���������ڵ������ķ��̣���������ĵ������伴�ɣ����ݺ����ĵ������жϼ��ɣ�
����ԭ����ʽת��Ϊblnx��m+$\frac{x}{2}$������[1��e]�Ϻ��������Ȼ�ú�����[1��e]�ϵ����������Ӷ���СֵΪ0���Ӷ�Ҫ����������ֻ��m+$\frac{x}{2}$��0���Ӷ��õ�-$\frac{x}{2}$��m��ͬ���İ취����[1��e]�ϵ���Сֵ��ֻҪ����Сֵ����m���Ӷ������m��ȡֵ��Χ
��� �⣺����m=1ʱ��g��x��=$\frac{1}{x}$+$\frac{1}{2}$��
��g�䣨x��=-$\frac{1}{{x}^{2}}$��
��k=g�䣨1��=-1��g��1��=1+$\frac{1}{2}$=$\frac{3}{2}$��
������y=g��x����x=1�������߷���Ϊy-$\frac{3}{2}$=-��x-1������2x+2y-5=0��
����f��x��=$\frac{lnx}{x}$�Ķ�����Ϊ��0��+�ޣ���
��f�䣨x��=$\frac{1-lnx}{{x}^{2}}$����f�䣨x��=0�����x=e��
��0��x��eʱ��f�䣨x����0������f��x������������
��x��eʱ��f�䣨x����0������f��x�������ݼ���
��2017��2016��
��$\frac{ln2017}{2017}$��$\frac{ln2016}{2016}$��
��ln2017${\;}^{\frac{1}{2017}}$��ln2016${\;}^{\frac{1}{2016}}$��
��2017${\;}^{\frac{1}{2017}}$��2016${\;}^{\frac{1}{2016}}$��
������������ʵ��b������x�IJ���ʽbf��x����g��x��������[1��e]�Ϻ������
��bxf��x����xg��x����
��blnx��m+$\frac{x}{2}$������[1��e]�Ϻ������
��b��0���ຯ��blnx��[1��e]�ϵ���������
��x=1ʱ������blnxȡ��Сֵ0��
��m+$\frac{x}{2}$��0��
��-$\frac{x}{2}$��m��x��[1��e]�Ϻ������-$\frac{x}{2}$��[1��e]�ϵ���СֵΪ-$\frac{e}{2}$��
��-$\frac{e}{2}$��m����m��-$\frac{e}{2}$
��ʵ��m��ȡֵ��ΧΪ��-�ޣ�-$\frac{e}{2}$����
���� ���⿼����ݵ����ļ������壬���������жϺ��������ԡ�������������ķ��������ݵ�������������Сֵ�������е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{47}{16}$��2] | B�� | [-$\frac{47}{16}$��$\frac{39}{16}$] | C�� | [-2$\sqrt{3}$��2] | D�� | [-2$\sqrt{3}$��$\frac{39}{16}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1��$\sqrt{2}$] | B�� | ��1��2] | C�� | [$\sqrt{2}$��+�ޣ� | D�� | [2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 6 | C�� | -1 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��1} | B�� | {x|x��1} | C�� | {x|0��x��1} | D�� | {x|x��1��x��-1} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
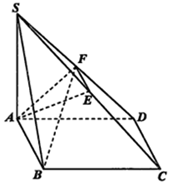 ��ͼ���ı���ABCDΪ���Σ�SA��ƽ��ABCD��E��F�ֱ���SC��SD���е㣬SA=AD=2��$AB=\sqrt{6}$
��ͼ���ı���ABCDΪ���Σ�SA��ƽ��ABCD��E��F�ֱ���SC��SD���е㣬SA=AD=2��$AB=\sqrt{6}$�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com