
分析 (Ⅰ)根据局部对称点的定义进行证明即可.
(Ⅱ)结合局部对称点的定义,结合指数函数的性质进行判断即可.
解答 解:(Ⅰ)证明:由f(x)=ax3+bx2+cx-b得f(-x)=-ax3+bx2-cx-b,
由f(-x)=-f(x) 得到关于x的方程2bx2-2b=0,…(1分)
当b≠0时,x=±1;当b=0,x∈R等式恒成立,
所以函数f(x)=ax3+bx2+cx-b必有局部对称点;…(4分)
(Ⅱ)∵f(x)=2x+m,∴f(-x)=2 -x+m
由f(-x)=-f(x) 得到关于x的方程2x+2-x+2m=0,…(6分)
因为f(x)的定义域为[-1,1],所以方程2x+2-x+2m=0在[-1,1]上有解.…(8分)
令t=2x∈$[\frac{1}{2},2]$,则$-2m=t+\frac{1}{t}∈[2,\frac{5}{2}]$,解得$m∈[-\frac{5}{4},-1]$.…(12分)
点评 本题主要考查函数与方程的应用,根据局部对称点的定义建立方程关系是解决本题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
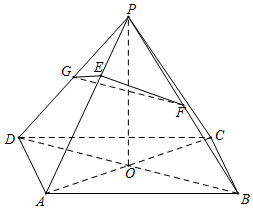 四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.
四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠DAB=$\frac{2π}{3}$,AC∩BD=O,且PO⊥平面ABCD,PO=$\sqrt{3}$,点F,G分别是线段PB,PD上的中点,E在PA上,且PA=3PE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com