
【题目】掷两颗质地均匀的骰子,在已知它们的点数不同的条件下,有一颗是6点的概率是 .
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() ﹣
﹣ ![]() ,则使得f(2x)>f(x﹣3)成立的x的取值范围是( )
,则使得f(2x)>f(x﹣3)成立的x的取值范围是( )
A.(﹣∞,﹣3)
B.(1,+∞)
C.(﹣3,﹣1)
D.(﹣∞,﹣3)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣t)|x|(t∈R).
(1)讨论y=f(x)的奇偶性;
(2)当t>0时,求f(x)在区间[﹣1,2]的最小值h(t).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若 ![]() ,试求f(x)在区间[﹣2,6]上的最值;
,试求f(x)在区间[﹣2,6]上的最值;
(3)是否存在m,使f(2( ![]() )2﹣4)+f(4m﹣2(
)2﹣4)+f(4m﹣2( ![]() ))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ ![]() ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
(1)求函数f(x)的极值;
(2)在曲线y=f(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1≠x2),使得直线AB的斜率k=f′( ![]() )?若存在,求出x1与x2的关系;若不存在,请说明理由.
)?若存在,求出x1与x2的关系;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查 结果如下表所示:
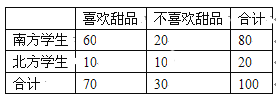
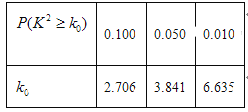
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
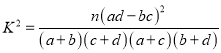 ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com