练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=(2cos2x-1)sin2x+cos4x

    （1）求f(x)的最小正周期及最大值。

    （2）设A,B,C为△ABC的三个内角，若cosB=,f()=-，且角A为钝角，求sinC

     

    (1)

    (2)

    【解析】(1)f(x)=(2cos2x-1)sin2x+cos4x

    =cos2xsin2x+cos4x

    =sin4x+cos4x

    =sin(4x+)

    ∴最小正周期T=

    当4x+=+2k(k∈Z)，即x=+(k∈Z)时,f(x)max=

    故最小正周期为，最大值为。

    （2）∵f()=-，

    ∴sin(4×+)=-sin(2A+)=-

    又A为钝角，所以2A+=，即A=

    由cosB=得，sinB=

    又sinC=sin[π-(A+B)]= =sin(A+B)=sinAcosB+cosAsinB

    =×+(-)×=

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科函数与方程（解析版） 题型：填空题

    关于x的实系数方程的一个根在区间[0，1]上，另一个根在区间[1，2]上，则2a+3b的最大值为 。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：填空题

    若＝xn＋…＋ax3＋bx2＋…＋1（n∈N*），且a∶b＝3∶1，那么n=_____．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科两角和与差的三角函数、倍角公式（解析版） 题型：选择题

    已知>0，函数f(x)=sin(x+)在(,)上单调递减，则的取值范围是（    ）

    A.[, ]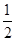

    B.[, ]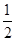

    C. [0,]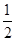

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科不等式选讲（解析版） 题型：解答题

    已知函数f(x)=|x－a|,其中a>1.

    (1)当a=2时,求不等式f(x)≥4－|x－4|的解集;

    (2)已知关于x的不等式|f(2x+a)－2f(x)|≤2的解集为{x|1≤x≤2},求a的值.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科三角函数的图象与性质（解析版） 题型：选择题

    设当x=θ时，函数f(x)＝sinx－2cosx取得最大值，则cosθ= (     )

    A.-

    B.

    C.-

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文解一元二次不等式、分式不等式、简单高次不等式（解析版） 题型：选择题

    不等式的解集是(　　)

    A.

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

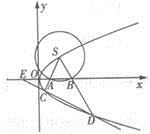
    如图，是抛物线为上的一点，以S为圆心，r为半径（）做圆，分别交x轴于A，B两点，连结并延长SA、SB，分别交抛物线于C、D两点。

    （1）求证：直线CD的斜率为定值；

    （2）延长DC交x轴负半轴于点E，若EC : ED = 1 : 3，求的值。

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科选择题专项训练（解析版） 题型：选择题

    若函数在区间[0,1]上的最小值等于-3，则实数的取值范围是 (    )

    A. B.

    C. D.

     

    查看答案和解析>>

    同步练习册答案