
已知数列{an}的前n项和Sn=n2(n∈N*),等比数列{bn}满足b1=a1,2b3=b4.
(1)求数列{an}和{bn}的通项公式;
(2)若cn=an·bn(n∈N*),求数列{cn}的前n项和Tn.
解析: (1)∵当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
∴an=2n-1(n∈N*),
∴b1=a1=1,设等比数列{bn}的公比为q,则q≠0.
∵2b3=b4,∴2q2=q3,∴q=2,
∴bn=2n-1(n∈N*).
(2)由(1)可得cn=an·bn=(2n-1)×2n-1(n∈N*),
∴Tn=1×20+3×2+5×22+…+(2n-1)×2n-1,①
∴2Tn=1×2+3×22+5×23+…+(2n-1)×2n,②
②-①得
Tn=(2n-1)×2n-(1×20+2×2+2×22+…+2×2n-1)
=(2n-1)×2n-(1+22+23+…+2n)
=(2n-3)×2n+3.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知数列{an}满足an+1=an-an-1(n≥2),a1=1,a2=3,记Sn=a1+a2+…+an,则下列结论正确的是( )
A.a100=-1,S100=5 B.a100=-3,S100=5
C.a100=-3,S100=2 D.a100=-1,S100=2
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数①f(x)=x2;②f(x)=ex;③f(x)=ln x;④f(x)=cos x.其中对于f(x)定义域内的任意一个x1都存在唯一的x2,使f(x1)f(x2)=1成立的函数是( )
A.① B.②
C.②③ D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
若点P(1,1)是圆x2+(y-3)2=9的弦AB的中点,则直线AB的方程为( )
A.x-2y+1=0 B.x+2y-3=0
C.2x+y-3=0 D.2x-y-1=0
查看答案和解析>>
科目:高中数学 来源: 题型:
某农场给某种农作物施肥量x(单位:吨)与其产量y(单位:吨)的统计数据如下表:
| 施肥量x | 2 | 3 | 4 | 5 |
| 产量y | 26 | 39 | 49 | 54 |
根据上表,得到回归直线方程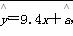 ,当施肥量x=6时,该农作物的预报产量是________.
,当施肥量x=6时,该农作物的预报产量是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系xOy中,双曲线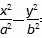 =1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
=1(a>0,b>0)的两条渐近线与抛物线y2=4x的准线相交于A,B两点.若△AOB的面积为2,则双曲线的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
某中学有4位学生申请A,B,C三所大学的自主招生.若每位学生只能申请其中一所大学,且申请其中任何一所大学是等可能的.
(1)求恰有2人申请A大学的概率;
(2)求被申请大学的个数X的概率分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
设全集为R,集合A={x|x≤3或x≥6},B={x|-2<x<9}.
(1) 求A∪B,(∁RA)∩B;
(2) 已知C={x|a<x<a+1},若C B,求实数a的取值范围.
B,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com