练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．下列运算结果中，正确的是（　　）
    A．a2a3=a5B．（-a2）3=（-a3）2C．（$\sqrt{a}$-1）0=1D．（-a2）3=a6

    分析 根据指数幂的运算性质即可求出答案．

    解答 解：a2a3=a2+3=a5，
    （-a2）3=-a6≠（-a3）2=a6，
    （$\sqrt{a}$-1）0=1，若成立，需要满足a≠1，
    （-a2）3=-a6，
    故正确的是A，
    故选：A．

    点评 本题考查了指数幂的运算性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．三棱锥P-ABC中各条棱长都相等，点E是BC中点，则直线PE与AB所成角的余弦值为$\frac{\sqrt{3}}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知数列{an}的前n项和为Sn=n2，数列{bn}的前n项和为 Tn=2bn-1．
    （1）求数列{an}与{bn}的通项公式；
    （2）求证：$\frac{1}{{{a_2}+{S_1}}}$+$\frac{1}{{a}_{3}+{S}_{2}}$+…+$\frac{1}{{{a_{n+1}}+{S_n}}}$＜$\frac{3}{4}$；
    （3）若满足不等式λbn-an+12＜0的正整数n有且仅有3个，求实数λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的两个焦点为F1，F2，点P在椭圆C上，且PF2⊥F1F2，|PF1|=$\frac{14}{3}$，|PF2|=$\frac{4}{3}$．
    （1）求椭圆C的方程；
    （2）若直线l过圆x2+y2+4x-2y=0的圆心M交椭圆于A，B两点，且A，B关于点M对称，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．如图，在边长为2的正方体ABCD-A1B1C1D1中，P、Q分别为棱AB、A1D1的中点，M、N分别为面BCC1B1和DCC1D1上的点，一质点从点P射向点M，遇正方体的面反射（反射服从光的反射原理），反射到点N，再经平面反射，恰好反射至点Q，则三条线段PM、MN、NQ的长度之和为（　　）
    A．$\sqrt{22}$B．$\sqrt{21}$C．2$\sqrt{5}$D．3$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知y=21+ax在R上是减函数，则a的取值范围是（-∞，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．某农民在一块耕地上种植一种作物，每年种植成本为800元，此作物的市场价格和这块地上的产量均具有随机性，且互不影响，其具体情况如下表：
    作物产量（kg）300500
    概率0.50.5
    作物市场价格（元/kg）610
    概率0.60.4
    （Ⅰ）设X表示该农民在这块地上种植1年此作物的利润，求X的分布列；
    （Ⅱ）若在这块地上连续3年种植此作物，求这3年中第二年的利润少于第一年的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知公差不为0的等差数列{an}的前n项和为Sn，满足a2，a3，a5成等比数列，S6=45．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）令pn=$\frac{{{S_{n+2}}}}{{{S_{n+1}}}}+\frac{{{S_{n+1}}}}{{{S_{n+2}}}}$，是否存在正整数M，使不等式p1+p2+…+pn-2n≤M恒成立，若存在，求出M的最小值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

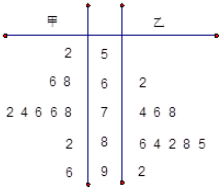
    12．某次数学测试后从两个班中各随机的抽取10名学生的数学成绩，作出它们的茎叶图如图所示，已知甲班的中位数为a1，标准差为s1，乙班的中位数为a2，标准差为s2，则由茎叶图可得（　　）
    A．a1＜a2，s1＞s2B．a1＜a2，s1＜s2C．a1＞a2，s1＞s2D．a1＞a2，s1＜s2

    查看答案和解析>>

    同步练习册答案