
 已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R
已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R分析 (1)由三角函数中的恒等变换应用化简函数解析式,利用函数y=Asin(ωx+φ)的图象变换即可得解;
(2)用五点法法作函数y=Asin(ωx+φ)在一个周期上的简图.
解答 解:(1)f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2
=$\sqrt{3}$sin2x+cos2x+1
=2sin(2x+$\frac{π}{6}$)+1,
将函数y=sinx的图象向左平移$\frac{π}{6}$个单位,再将所得图象上每一点的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变式),把图象上各点纵坐标伸长到原来的2倍(横坐标不变),最后把得到的图象向上平移1个单位长度,得到函数f(x)的图象.
(2)由于 0≤x≤π,∴$\frac{π}{6}$≤2x+$\frac{π}{6}$≤$\frac{13π}{6}$,列表:
| 2x+$\frac{π}{6}$ | $\frac{π}{6}$ | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π | $\frac{13π}{6}$ |
| x | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ | π |
| f(x) | 1 | 2 | 0 | -2 | 0 | 1 |
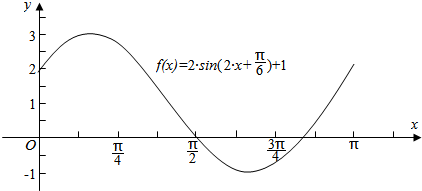
点评 本题主要考查了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,用五点法法作函数y=Asin(ωx+φ)在一个周期上的简图,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)的最小正周期为2π | B. | f(x)的最大值为-1 | ||
| C. | f(x)是偶函数 | D. | f(x)在[$\frac{π}{12}$,$\frac{π}{4}$]上单调增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | $-\frac{1}{6}$ | C. | 6 | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
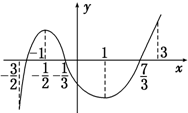 已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].
已知函数y=f(x)在定义域$({-\frac{3}{2},3})$上可导,其图象如图,记y=f(x)的导函数y=f′(x),则不等式xf′(x)≤0的解集是[0,1]∪(-$\frac{3}{2}$,-$\frac{1}{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
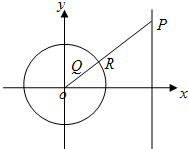 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
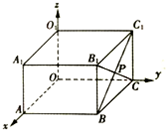 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )| A. | (6,2,1) | B. | (1,2,6) | C. | (4,6,2) | D. | (2,6,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com