
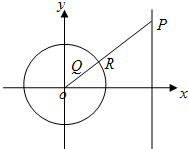
 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.分析 (1)通过将x=ρcosθ、y=ρsinθ 分别代入圆C、直线l方程即可;
(2)通过设点Q(x,y),P(4,t),利用OP、OQ斜率相等即得P(4,4×$\frac{y}{x}$),结合|OR|=2、利用|OQ|•|OP|=|OR|2计算即可.
解答 解:(1)将x=ρcosθ、y=ρsinθ 代入圆C:x2+y2=4,
可得:ρ2=4,
即圆C的极坐标方程为:ρ=2;
将x=ρcosθ、y=ρsinθ 代入直线l:x=8,
可得l的极坐标方程为:ρcosθ=8;
(2)设点Q(x,y),P(4,t),显然x>0,
∵P、Q共线,
∴P、Q为同一角的终边上,
∵直线l:x=8,
∴$\frac{y}{x}$=$\frac{t}{4}$,∴P(4,4×$\frac{y}{x}$),
又∵R在圆C:x2+y2=4上,
∴|OR|=2,
∵|OQ|•|OP|=|OR|2,
∴$\sqrt{{x}^{2}+{y}^{2}}$•$\sqrt{{4}^{2}+(\frac{4y}{x})^{2}}$=22,
整理得:x2-x+y2=0,
∴(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$(x>0),
∴点Q在直角坐标系下的轨迹方程为:(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$(x>0).
点评 本题主要考查坐标系与方程,直线、椭圆的方程和性质,曲线与方程的关系,轨迹的概念和求法,利用方程判定曲线的性质等解析几何的基本思想和综合运用知识的能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 2$\sqrt{13}$π+6 | B. | 2π+6 | C. | $6+(2\sqrt{13}+2)π$ | D. | $6+(\sqrt{13}+2)π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R
已知函数f(x)=$\sqrt{3}sin2x-2{sin^2}$x+2,x∈R查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ | q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{5}$,1) | B. | [-$\sqrt{5}$,1) | C. | [-2,1) | D. | (-2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com