
| A. | (-$\sqrt{5}$,1) | B. | [-$\sqrt{5}$,1) | C. | [-2,1) | D. | (-2,1) |
分析 根据题意求出函数的导数,因为函数f(x)在区间(m,6-m2)上有最小值,所以f′(x)先小于0然后再大于0,所以结合二次函数的性质可得:m<1<6-m2,进而求出正确的答案.
解答 解:函数y=f(x)=x3-3x,
即有f′(x)=3x2-3.
令f′(x)=3x2-3=0可得,x=±1;
因为函数f(x)在区间(m,6-m2)上有最小值,其最小值为f(1),
所以函数f(x)在区间(m,6-m2)内先减再增,即f′(x)先小于0然后再大于0,
所以结合二次函数的性质可得:m<1<6-m2,
且f(m)=m3-3m≥f(1)=-2,且6-m2-m>0,
联立解得:-2≤m<1.
故选:C.
点评 解决此类问题的关键是熟练掌握导数的应用,即求函数的单调区间与函数的最值,并且进行正确的运算.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
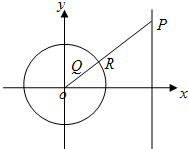 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 玩具名称 | A | B | C |
| 工时(分钟) | 5 | 7 | 4 |
| 利润(元) | 5 | 6 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | $[{-\sqrt{2},1}]$ | C. | $[{-1,\sqrt{2}}]$ | D. | $[{-\sqrt{2},\sqrt{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{9}{14}$ | C. | $\frac{5}{8}$ | D. | $\frac{14}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com