考点:数列递推式,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)把题目给出的数列递推式取倒数,即可证明数列{
+
}是等比数列,由等比数列的通项公式求得
+
,则数列{a
n}的通项a
n的通项可求;
(2)把数列{a
n}的通项a
n代入b
n=(3
n-1)
a
n,由错位相减法求得数列{b
n}的前n项和为T
n,作差后得到T
n为递增数列.然后对n分类求得满足不等式(-1)
nλ<T
n的实数λ的范围,则答案可求.
解答:
(1)证明:由a
n+1=
(n∈N
*),
得
==+1,
∴
+=3(+).
∴数列{
+}是以3为公比以
(+)=为首项的等比数列.
(2)解:由(1)知,
bn=(3n-1)•=n•()n-1,
Tn=1×1+2×()1+3×()2+…+n•()n-1,
Tn=1×+2×()2+…+(n-1)()n-1+n()n,
两式相减得,
Tn=1+++…+-=
-=2-,
∴
Tn=4-.
∵
Tn+1-Tn=(4-)-(4-)=
>0,
∴T
n为递增数列.
①当n为正奇数时,-λ<T
n对一切正奇数成立,
∵
(Tn)min=T1=1=T
1=1,∴-λ<1,∴λ>-1;
②当n为正偶数时,λ<T
n对一切正偶数成立,
∵
(Tn)min=T2=2=T
2=2,∴λ<2.
综合①②知,-1<λ<2.
点评:本题考查数列递推式,考查了等比关系的确定,训练了错位相减法求数列的前n项和,考查了利用分类讨论的数学思想方法求解数列不等式,是中档题.



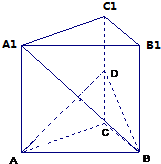 如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AC=BC=2,∠ACB=90°,侧棱AA1=2,D是CC1的中点.