考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)由题意可得函数的最小正周期T=2×
=
,解得ω=1,可得f(x)=sin(2x+
).令2kπ-
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的增区间.
(2)由f(α)=sin(2α+
)=
,2α+
∈[-
,
],求得cos(2α+
)的值,再由f(α+
)=sin(2α+
)=cos2α=cos[(2α+
)-
],利用两角差的余弦公式计算求得结果.
(3)由题意可得即2cos
2x+mcosx+2=0,在x∈(0,
)有实数解.令cosx=t∈(0,1),则2t
2+mt+2=0在(0,1)上有解.令g(t)=2t
2+mt+2,利用二次函数的性质求得m的范围.
解答:
解:(1)∵函数f(x)=sin(2ωx+
)(ω>0),直线x=x
1、x=x
2是y=f(x)图象的两条对称轴,
且|x
1-x
2|的最小值为
,
∴函数的最小正周期T=2×
=
,解之得ω=1,故f(x)=sin(2x+
).
令2kπ-
≤2x+
≤2kπ+
,k∈z,求得kπ-
≤x≤kπ+
,
故函数的增区间为[kπ-
,kπ+
],k∈z.
(2)∵f(α)=sin(2α+
)=
,α∈[-
,
],∴2α+
∈[-
,
],
∴cos(2α+
)=
,
求得 f(α+
)=sin(2α+
)=cos2α=cos[(2α+
)-
]=cos(2α+
)cos
+sin(2α+
)sin
=
×
+
×=
.
(3)关于x的方程f(x+
)+mcosx+3=0,即 cos2x+mcosx+3=0,
即2cos
2x+mcosx+2=0,在x∈(0,
)有实数解.
令cosx=t∈(0,1),则2t
2+mt+2=0在(0,1)上有解.
令g(t)=2t
2+mt+2,∵△=m
2-16≥0,∴m≥4,或m≤-4.
由于对称轴为t=-
≥1,或 t=-
≤-1,
∵g(0)=2>0,∴由图象可得 g(1)=m+4<0,解得m<-4.

点评:本题主要考查正弦函数的图象和性质,三角恒等变换,二次函数的性质应用,属于中档题.





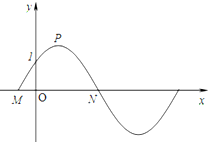 已知如图,函数y=2sin(
已知如图,函数y=2sin(