已知函数f(x)=ax+lnx,x∈(1,e),且f(x)有极值.
(1)求实数a的取值范围;
(2)求函数f(x)的值域;
(3)函数g(x)=x3-x-2,证明:?x1∈(1,e),?x0∈(1,e),使得g(x0)=f(x1)成立.
分析:(1)由f(x)=ax+lnx求导,再由f(x)有极值知f′(x)=0解,且在两侧导函数正负相异求解.
(2)由(Ⅰ)可知f(x)的极大值为
f(-)=-1+ln(-),再求得端点值f(1)=a,f(e)=ae+1,比较后取最小值和最大值,从而求得值域.
(3)证明:由:?x
1∈(1,e),?x
0∈(1,e),使得g(x
0)=f(x
1)f(x
1)即研究:f(x)的值域是g(x)的值域的子集,所以分别求得两函数的值域即可.
解答:解:(1)由f(x)=ax+lnx求导可得:
f′(x)=a+.(2分)
令
f′(x)=a+=0,可得
a=-∵x∈(1,e),∴
-∈(-1,-)∴
a∈(-1,-)(3分)
又因为x∈(1,e)
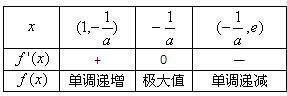
所以,f(x)有极值所以,实数a的取值范围为
(-1,-).(4分)
(2)由(Ⅰ)可知f(x)的极大值为
f(-)=-1+ln(-)(6分)
又∵f(1)=a,f(e)=ae+1
由a≥ae+1,解得
a≤又∵
-1<<-∴当
-1<a≤时,
函数f(x)的值域为(ae+1,-1+ln(
-)](8分)
当
<a<-时,
函数f(x)的值域为(a,-1+ln(
-)].(10分)
(3)证明:由g(x)=x
3-x-2求导可得g'(x)=3x
2-1(11分)
令g'(x)=3x
2-1=0,解得
x=±令g'(x)=3x
2-1>0,解得
x<-或
x>又∵
x∈(1,e)⊆(,+∞)∴g(x)在(1,e)上为单调递增函数(12分)
∵g(1)=-2,g(e)=e
3-e-2
∴g(x)在x∈(1,e)的值域为(-2,e
3-e-2)(14分)
∵
e3-e-2>-1+ln(-),
-2<ae+1,-2<a
∴
(ae+1,-1+ln(-)]⊆(-2,e3-e-2),
(a,-1+ln(-)]⊆(-2,e3-e-2)∴?x
1∈(1,e),?x
0∈(1,e),使得g(x
0)=f(x
1)成立.(16分)
点评:本题主要考查用导数来研究函数的单调性,极值,最值等问题,以及集合思想的应用.




 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案