
分析 设A={x|2a≤x≤a2+1},B={x|(x-2)[x-(3a+1)]≤0},由于p是q的充分条件,可得A⊆B.
(1)当a≥$\frac{1}{3}$时,此时B={x|2≤x≤3a+1},可得$\left\{\begin{array}{l}{2a≥2}\\{{a}^{2}+1≤3a+1}\end{array}\right.$.
(2)当a<$\frac{1}{3}$时,B={x|3a+1≤x≤2},可得$\left\{\begin{array}{l}{2a≥3a+1}\\{{a}^{2}+1≤2}\end{array}\right.$.
解答 解:x2-3(a+1)x+6a+2≤0,化为(x-2)[x-(3a+1)]≤0,
设A={x|2a≤x≤a2+1},B={x|(x-2)[x-(3a+1)]≤0},∵p是q的充分条件,∴A⊆B.
(1)当a≥$\frac{1}{3}$时,B={x|2≤x≤3a+1},∴$\left\{\begin{array}{l}{2a≥2}\\{{a}^{2}+1≤3a+1}\end{array}\right.$,解得1≤a≤3.
(2)当a<$\frac{1}{3}$时,B={x|3a+1≤x≤2},∴$\left\{\begin{array}{l}{2a≥3a+1}\\{{a}^{2}+1≤2}\end{array}\right.$,解得a=-1.
∴实数a取值范围是{a|1≤a≤3,或a=-1}.
点评 本题考查了不等式的性质、简易逻辑的判定方法、集合的运算性质,考查了推理能力与计算能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -cos160° | B. | cos160° | C. | $\frac{1}{cos160°}$ | D. | $\frac{1}{-cos160°}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个球都是白球的概率 | B. | 2个球中恰好有1个是白球的概率 | ||
| C. | 2个球都不是白球的概率 | D. | 2个球至少有一个白球的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{4}$,$\frac{2π}{3}$] | B. | [-$\frac{π}{8}$,$\frac{π}{4}$] | C. | [-$\frac{π}{8}$,$\frac{2π}{3}$] | D. | [0,$\frac{2π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{2}{3}$ | C. | $\frac{25}{13}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
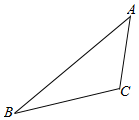 在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.
在△ABC中,AC=$\sqrt{2}$,AB=$\sqrt{3}$+1,∠BAC=45°,点P满足:$\overrightarrow{BP}$=(1-λ)$\overrightarrow{BA}$+λ$\overrightarrow{BC}$(λ>0),AP=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com