考点:数列递推式
专题:等差数列与等比数列
分析:(1)采用叠加法求数列的通项公式.
(2)采用叠乘法求数列的通项公式.
(3)采用构造新数列法求数列的通项公式.
(4)采用前n项和法求数列的通项公式.
(5)采用前n项和与叠乘法求数列的通项公式.
解答:
解:(1)a
1=1,a
n=a
n-1+2n-1(n≥2),
则:a
n-a
n-1=2n-1
a
n-1-a
n-2=2(n-1)-1
…
a
2-a
1=2•2-1
所以:a
n-a
1=2(2+3+…+n)-n
an=2•-2-n+1整理得:
an=n2-1(2)a
1=1,a
n+1=
a
n,
则:
==…
=所以:
=解得:
an=(3)a
1=1,a
n=2a
n-1+1(n≥2),
则:
=2,所以数列{a
n+1}是以a
1+1为首项,公比为2的等比数列.
an+1=(a1+1)2n-1则:
an=2n-1当n=1时符合此通项公式
所以:
an=2n-1(4)数列前n项和S
n=3n
2+n+1,
则:
Sn-1=3(n-1)2+(n-1)+1(n≥2)
a
n=S
n-S
n-1=6n-2
a
1=5,不符合此通项公式,
所以:
an=(5)a
1=
,S
n=n
2a
n,①
则
Sn-1=(n-1)2an-1②
①-②得:
=则:采用(2)的方法
即得:
an=
点评:本题考查的知识要点:利用叠加和叠乘法,前n项和法求数列的通项公式,属于基础题型.



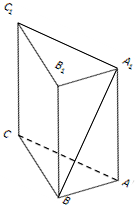 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2