
【题目】已知数列![]() 与
与![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)设![]() 的第
的第![]() 项是最大项,即
项是最大项,即![]() ,求证:
,求证:![]() 的第
的第![]() 项是最大项;
项是最大项;
(3)设![]() ,求
,求![]() 的取值范围,使得
的取值范围,使得![]() 有最大值
有最大值![]() 与最小值
与最小值![]() ,且
,且![]() .
.
【答案】(1)![]() (2)证明见解析(3)
(2)证明见解析(3)![]()
【解析】
(1)把bn=3n+5代入已知递推式可得an+1﹣an=6,由此得到{an}是等差数列,则an可求;
(2)由an=(an﹣an﹣1)+(an﹣1﹣an﹣2)+…+(a2﹣a1)+a1,结合递推式累加得到an=2bn+a1﹣2b1,求得![]() ,进一步得到
,进一步得到![]() 得答案;
得答案;
(3)由(2)可得![]() ,然后分﹣1<λ<0,λ=﹣1,λ<﹣1三种情况求得an的最大值M和最小值m,再由
,然后分﹣1<λ<0,λ=﹣1,λ<﹣1三种情况求得an的最大值M和最小值m,再由![]() ∈(﹣2,2)列式求得λ的范围.
∈(﹣2,2)列式求得λ的范围.
(1)由![]() 可得:
可得:![]() ,又
,又![]() ,所以数列
,所以数列![]() 以1为首项,6为公差的等差数列,即有
以1为首项,6为公差的等差数列,即有![]() ;
;
(2)由![]() 可得:
可得:
![]()
![]()
……
![]() ,
,
将上述式子累加可得
![]() ,当
,当![]() 时,也成立,所以
时,也成立,所以![]() ,由此可得
,由此可得
![]() ,由于
,由于![]() 为常数,所以当
为常数,所以当![]() 的第
的第![]() 项是最大项时,
项是最大项时,![]() 最大,即
最大,即![]() 的第
的第![]() 项是最大项;
项是最大项;
(3)由(2)可知![]() ,即
,即![]() ,结合
,结合![]() 可得
可得
![]() ,分三种情况进行讨论:
,分三种情况进行讨论:
①当![]() 时,则
时,则![]() 为偶数时
为偶数时![]() ,
,![]() 为奇数时,
为奇数时,![]() ,即
,即![]() ,此时
,此时![]() ,由此,此情况不符合条件;
,由此,此情况不符合条件;
②当![]() 时,则
时,则![]() 为偶数时,
为偶数时,![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() “随着
“随着![]() 增大值减小,此时
增大值减小,此时![]() ,
,![]() ,无最小值(无限靠近0);
,无最小值(无限靠近0);![]() 为奇数,
为奇数,![]() ,此时
,此时![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值减小,结合
增大值减小,结合![]() ,可知随着
,可知随着![]() 增大
增大![]() 值增大,此时
值增大,此时![]() ,无最大值(无限靠近0);由此可知数列
,无最大值(无限靠近0);由此可知数列![]() 的最大值
的最大值![]() ,最小值
,最小值![]() ,
,![]() ,又
,又![]() ,所以
,所以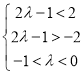 ,解之
,解之![]() ;
;
③当![]() 时,则
时,则![]() 为偶数时,
为偶数时,![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值增大,此时
增大值增大,此时![]() ,
,![]() ,无最大值(无限靠近
,无最大值(无限靠近![]() );
);![]() 为奇数时,
为奇数时,![]() ,此时
,此时![]() ,由于
,由于![]() ,所以
,所以![]() ,从而
,从而![]() 随着
随着![]() 增大值增大,结合
增大值增大,结合![]() ,可知随着
,可知随着![]() 增大
增大![]() 值减小,此时
值减小,此时![]() ,无最小值(无限靠近
,无最小值(无限靠近![]() );由此可知,在
);由此可知,在![]() 条件下,数列
条件下,数列![]() 无最值,显然不符合条件;
无最值,显然不符合条件;
综上,符合条件的实数![]() 的取值范围为
的取值范围为![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
【题目】在一次数学考试中,从甲,乙两个班级各抽取10名同学的成绩进行统计分析,他们成绩的茎叶图如图所示,成绩不小于90分为及格.

(1)从两班10名同学中各抽取一人,在有人及格的情况下,求乙班同学不及格的概率;
(2)从甲班10人中取一人,乙班10人中取两人,三人中及格人数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
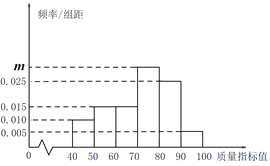
(1)求出直方图中![]() 的值;
的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义在
是定义在![]() 上的“
上的“![]() 类函数”,求是实数
类函数”,求是实数![]() 的最小值;
的最小值;
(3)若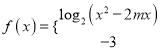
![]() 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 上,
上,![]() ,且当
,且当![]() 时,恒有
时,恒有![]() ,又数列
,又数列![]() 满足
满足![]() ,
,![]() ,设
,设![]() ,对于任意的
,对于任意的![]() ,
,![]() 的最小自然数
的最小自然数![]() 的值为_______________________________.
的值为_______________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①命题“若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于2”的逆命题是真命题
中至少有一个不小于2”的逆命题是真命题
②命题“设![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”是一个真命题
”是一个真命题
③“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
④已知![]() ,
,![]() 都是实数,“
都是实数,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() ,
,![]() 满足
满足![]() ,则称
,则称![]() 为数列
为数列![]() 的“偏差数列”.
的“偏差数列”.
(1)若![]() 为常数列,且为
为常数列,且为![]() 的“偏差数列”,试判断
的“偏差数列”,试判断![]() 是否一定为等差数列,并说明理由;
是否一定为等差数列,并说明理由;
(2)若无穷数列![]() 是各项均为正整数的等比数列,且
是各项均为正整数的等比数列,且![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,求
的“偏差数列”,求![]() 的值;
的值;
(3)设![]() ,
,![]() 为数列
为数列![]() 的“偏差数列”,
的“偏差数列”,![]() ,
,![]() 且
且![]() 若
若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com