
分析 将双曲线化成标准方程:$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{3}$=1,可知焦点在y轴上,c=$\sqrt{7}$,即可求得焦点坐标.
解答 解:由题意可知:$\frac{{y}^{2}}{4}$-$\frac{{x}^{2}}{3}$=1,
∴双曲线的焦点在y轴上,c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{4+3}$=$\sqrt{7}$,
∴双曲线的焦点坐标为:(0,$\sqrt{7}$),(0,-$\sqrt{7}$),
故答案为:(0,$\sqrt{7}$),(0,-$\sqrt{7}$).
点评 本题考查双曲线的标准方程及简单几何性质,考查转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | (3,+∞) | C. | $[{-\frac{2}{3},\frac{1}{3}}]$ | D. | $[{-\frac{1}{3},\frac{2}{3}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (-∞,2)∪(2,3] | C. | (-∞,2)∪(2,3) | D. | (3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
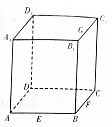 已知点E、F、G分别为正方体ABCD-A1B1C1D1的棱AB、BC、$B_1^{\;}{C_1}$的中点,如图,则下列命题为假命题的是( )
已知点E、F、G分别为正方体ABCD-A1B1C1D1的棱AB、BC、$B_1^{\;}{C_1}$的中点,如图,则下列命题为假命题的是( )| A. | 点P在直线FG上一定,总有AP⊥DE | |
| B. | 点Q在直线BC1上运动时,三棱锥A-D1QC的体积为定值 | |
| C. | 点M是正方体面A1B1C1D1内的点到点D和点C1距离相等的点,则M的轨迹是一条直线 | |
| D. | 过F,D1,G的截面是正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com