
 。同样也假定D受A、B和C感染的概率都是
。同样也假定D受A、B和C感染的概率都是 。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
。在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。科目:高中数学 来源:不详 题型:解答题
 .
. 的概率;
的概率; 的概率P;
的概率P;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 存活数 | 死亡数 | 合计 |
| 新措施 | 132 | 18 | 150 |
| 对照 | 114 | 36 | 150 |
| 合计 | 246 | 54 | 300 |
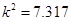 ,故我们由此认为 “新措施对防治非典有效” 的把握为( )
,故我们由此认为 “新措施对防治非典有效” 的把握为( )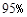 C.
C.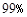 D.
D.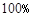
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为
进入下一轮考核,否则被淘汰,已知某选手能正确回答第一、二、三、四轮问题的概率分别为 、
、 、
、 、
、 ,且各
,且各 轮问题能否正确回答互不影响。
轮问题能否正确回答互不影响。 个数记为
个数记为 ,求随机变量
,求随机变量 的分布列和期望。
的分布列和期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com