Question

4．在?ABCD中，AB=4$\sqrt{6}$cm，AD=4$\sqrt{3}$cm，∠A=45°，求这个四边形两条对角线的长度和平行四边形的面积．

Answer 1

分析 根据余弦定理即可求出四边形两条对角线的长度，再根据平行四边形的面积公式计算即可．

解答 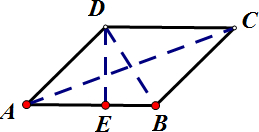解：连接AC，BD，过点D做DE⊥AB，垂足为E，如图所示，
∵四边形ABCD为平行四边形，∠A=45°，
∴∠B=135°，BC=AD=AD=4$\sqrt{3}$cm，
根据余弦定理，得
（BD）²=（AD）²+（AB）²-2AD•ABcosA，（AC）²=（BC）²+（AB）²-2BC•ABcosB，
∴（BD）²=（4$\sqrt{3}$）²+（4$\sqrt{6}$）²-2×$4\sqrt{3}$×4$\sqrt{6}$cos45°=（4$\sqrt{3}$）²，（AC）²=（4$\sqrt{3}$）²+（4$\sqrt{6}$）²-2×$4\sqrt{3}$×4$\sqrt{6}$cos135°=16×15，
∴BD=4$\sqrt{3}$，AC=4$\sqrt{15}$，
在Rt△DEA中，DE=ADsinA=4$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=2$\sqrt{6}$cm，
∴S_ABCD=AB•DE=4$\sqrt{6}$×2$\sqrt{6}$=48cm²，
（或者S_ABCD=2S_△ABD=2×$\frac{1}{2}$AB•AD•ADsinA=48cm²）．

点评 本题考查了余弦定理和三角形的面积公式，属于基础题．