
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上,
)=a,且点A在直线l上,
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
【答案】
(1)解:点A( ![]() ,
, ![]() )在直线l上,得
)在直线l上,得 ![]() cos(θ﹣
cos(θ﹣ ![]() )=a,∴a=
)=a,∴a= ![]() ,
,
故直线l的方程可化为:ρsinθ+ρcosθ=2,
得直线l的直角坐标方程为x+y﹣2=0
(2)解:消去参数α,得圆C的普通方程为(x﹣1)2+y2=1
圆心C到直线l的距离d= ![]() <1,
<1,
所以直线l和⊙C相交
【解析】(1)根据点A在直线l上,将点的极坐标代入直线的极坐标方程即可得出a值,再利用极坐标转化成直角坐标的转换公式求出直线l的直角坐标方程;(2)欲判断直线l和圆C的位置关系,只需求圆心到直线的距离与半径进行比较即可,根据点到线的距离公式求出圆心到直线的距离然后与半径比较.
【考点精析】利用直线的参数方程对题目进行判断即可得到答案,需要熟知经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为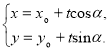 (
(![]() 为参数).
为参数).


科目:高中数学 来源: 题型:
【题目】某校初三(1)班、(2)班各有49名学生,两班在一次数学测验中的成绩统计如下表: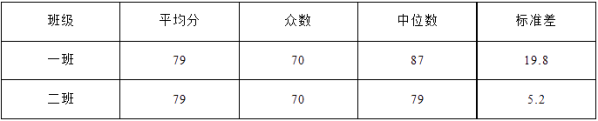
(1)请你对下面的一段话给予简要分析:
高一(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均分为79分,得70分的人最多,我得了85分,在班里算上上游了!”
(2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=﹣1时函数y=g(x)取得极值,确定y=g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要分析学生初中升学考试的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽取10名学生,分析他们入学的数学成绩(x)和高一年级期末数学考试成绩(y)(如下表):
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
y | 65 | 78 | 52 | 85 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)画出散点图;
(2)判断入学成绩(x)与高一期末考试成绩(y)是否有线性相关关系;
(3)如果x与y具有线性相关关系,求出回归直线方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经问卷调查,某班学生对摄影分别执“喜欢”“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的是5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那全班学生中“喜欢”摄影的比全班学生人数的一半还多人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且对任意a、b∈R,当a+b≠0时,都有 ![]() .
.
(1)若a>b,试比较f(a)与f(b)的大小关系;
(2)若f(1+m)+f(3-2m)≥0,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com