
【题目】求下列各曲线的标准方程
(1)实轴长为12,离心率为 ![]() ,焦点在x轴上的椭圆;
,焦点在x轴上的椭圆;
(2)焦点是双曲线16x2﹣9y2=144的左顶点的抛物线.
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M,N分别为PB,AC的中点, 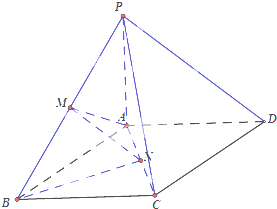
(1)求证:MN∥平面PAD;
(2)求点B到平面AMN的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,已知点A的极坐标为( ![]() ,
, ![]() ),直线l的极坐标方程为ρcos(θ﹣
),直线l的极坐标方程为ρcos(θ﹣ ![]() )=a,且点A在直线l上,
)=a,且点A在直线l上,
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为 ![]() (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在斜三棱柱 ![]() 中,∠BAC=90°,BC1⊥AC,则点C1在平面ABC上的射影H必在( )
中,∠BAC=90°,BC1⊥AC,则点C1在平面ABC上的射影H必在( )
A.直线AB上
B.直线BC上
C.直线AC上
D.△ABC的内部
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在平行四边形ABCD中,已知AD=2AB=2a,BD= ![]() ,AC∩BD=E,将其沿对角线BD折成直二面角.
,AC∩BD=E,将其沿对角线BD折成直二面角.

求证:
(1)AB⊥平面BCD;
(2)平面ACD⊥平面ABD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2+bx+c(a,b,c∈R),若函数y=f(x)ex在x=﹣1处取得极值,则下列图象不可能为y=f(x)的图象是( )
A.
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有2名男生和3名女生. (Ⅰ)若其中2名男生必须相邻排在一起,则这5人站成一排,共有多少种不同的排法?
(Ⅱ)若男生甲既不能站排头,也不能站排尾,这5人站成一排,共有多少种不同的排法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com