
分析 (1)设数列{an}的公差为d,由题意可得d>0,运用等差数列的性质和通项公式,计算即可得到;
(2)求出数列{bn}的通项,再由错位相减法,即可得到前n项和Sn.
解答 解:(1)设数列{an}的公差为d,由题意可得d>0,
由a2+a7=9,a4•a5=20,
可得a4+a5=9,a4•a5=20,a4<a5,
解得a4=4,a5=5,
可得d=5-4=1,
即有an=4+n-4=n;
(2)bn=$\frac{n}{{2}^{{a}_{n}}}$=$\frac{n}{{2}^{n}}$,
前n项和Sn=$\frac{1}{2}$+$\frac{2}{{2}^{2}}$+$\frac{3}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n-1}}$+$\frac{n}{{2}^{n}}$,
$\frac{1}{2}$Sn=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+$\frac{3}{{2}^{4}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,
两式相减,可得$\frac{1}{2}$Sn=$\frac{1}{2}+$$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$,
可得Sn=2-$\frac{n+2}{{2}^{n}}$.
点评 本题考查等差数列的性质和通项公式的运用,同时考查数列的求和方法:错位相减法,及等比数列的求和公式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 16(1-4-n) | B. | 16(1-2n) | C. | $\frac{32}{3}(1-{4^{-n}})$ | D. | $\frac{32}{3}(1-{2^{-n}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | e2 | C. | $\frac{\sqrt{3}}{3}$ | D. | e-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
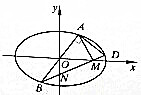 对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:
对于椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),c为椭圆半焦距,e为椭圆离心率,过原点O的直线与椭圆C交于A、B两点(A、B不是椭圆C的顶点),点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M、N两点,证明:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com