
分析 分析表达式,构造两个新函数F(x)=e2x-lnx与φ(x)=$\frac{lnx}{x}+\frac{5}{2}$,而后求证F(x)min>φ(x)max.
解答 解:令F(x)=e2x-lnx
对F(x)求导:F'(x)=${e}^{2}-\frac{1}{x}$
令F'(x)=0⇒x0=$\frac{1}{{e}^{2}}$
∴F(x)在(0,$\frac{1}{{e}^{2}}$)上单调递减,($\frac{1}{{e}^{2}}$,+∞)上单调递增;
所以,F(x)min=F($\frac{1}{{e}^{2}}$)=3.
令$ϕ(x)=\frac{lnx}{x}+\frac{5}{2},x∈(0,e]$,$ϕ'(x)=\frac{1-lnx}{x^2}$
当x∈(0,e]时,ϕ'(x)≥0;
∴f(x)在(0,e]上单调递增;
∴$ϕ{(x)_{max}}=ϕ(e)=\frac{1}{e}+\frac{5}{2}<\frac{1}{2}+\frac{5}{2}=3$;
∴${e^2}x-lnx>\frac{lnx}{x}+\frac{5}{2}$;
即${e^2}{x^2}-\frac{5}{2}x>(x+1)lnx$.
点评 本题主要考查利用构造新函数的方式来证明不等式成立,考查函数的单调性,属于中等难度题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
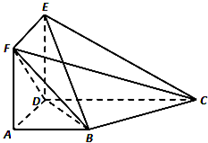 如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$
如图,多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=2,CD=4,直线BE与平面ABCD所成的角的正切值等于$\frac{\sqrt{2}}{2}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com