已知i是虚数单位.若|a-i|=$\sqrt{3}$a.则实数a=$\frac{\sqrt{2}}{2}$．题目和参考答案——青夏教育精英家教网—

10．已知i是虚数单位，若|a-i|=$\sqrt{3}$a，则实数a=$\frac{\sqrt{2}}{2}$．

分析利用复数的模的计算公式建立方程，即可得出实数a．

解答解：∵|a-i|=$\sqrt{3}$a，
∴|$\sqrt{{a}^{2}+1}$|=$\sqrt{3}$a，＞0，化为a²=$\frac{1}{2}$，a＞0，解得a=$\frac{\sqrt{2}}{2}$．
故答案为：$\frac{\sqrt{2}}{2}$．

点评本题考查了复数的模的计算公式，考查了计算能力，属于基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：填空题

20．设随机变量X～B（8，$\frac{3}{4}$），则D（X）=$\frac{3}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

1．

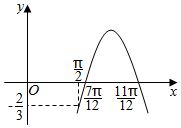函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，且f（$\frac{π}{2}$）=-$\frac{2}{3}$，则函数f（x）的表达式为（　　）

A．

f（x）=$\frac{2}{3}$cos（3x-$\frac{π}{4}$）

B．

f（x）=$\frac{2}{3}$cos（3x+$\frac{π}{4}$）

C．

f（x）=$\frac{2}{3}$$\sqrt{2}$cos（3x+$\frac{π}{4}$）

D．

f（x）=$\frac{2}{3}$$\sqrt{2}$cos（3x-$\frac{π}{4}$）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．作出下面函数的图象，并根据图象写出单调区间．
（1）y=|x²-1|；
（2）y=-x²+2|x|-3．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

5．在△ABC中，cos²B＞cos²A是A＞B的（　　）

A．

充分条件

B．

充分不必要条件

C．

充要条件

D．

必要不充分条件

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．模拟考试后，某校对甲、乙两个班的数学考试成绩进行分析，规定：不少于120分为优秀，否则为非优秀，统计成绩后，得到如下的2×2列联表，已知在甲、乙两个班全部100人中随机抽取1人为优秀的概率为$\frac{3}{10}$．

	优秀	非优秀	合计
甲班	20	30	50
乙班	10	40	50
合计	30	70	100

（1）请完成上面的2×2列联表；
（2）根据列联表的数据，若按97.5%的可靠性要求，能否认为“成绩与班级有关系”？
（3）在“优秀”的学生人中，用分层抽样的方法抽取6人，再平均分成两组进行深入交流，求第一组中甲班学生人数ξ的分布列和数学期望．
参考公式与临界值表：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$