
| ���� | ������ | �ϼ� | |
| �װ� | 20 | 30 | 50 |
| �Ұ� | 10 | 40 | 50 |
| �ϼ� | 30 | 70 | 100 |
| P��K2��k�� | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���� ��1�����Ұ����������Ϊx�ˣ����ݼס���������ȫ��100���������ȡ1��Ϊ����ĸ���Ϊ$\frac{3}{10}$�г����̣�������̵Ľ�õ�x��ֵ��ȷ�����Ұ���װ������������д���ɣ�
��2����a��b��c��d��ֵ����K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$������õ���������������жϣ�
��3������ֲ�����м������������������ȷ�����ε�ֵ������ȷ�����εķֲ��У����������ѧ����E�Σ�
��� �⣺��1�����Ұ����������Ϊx�ˣ�
��������ã�$\frac{20+x}{100}$=$\frac{3}{10}$��
��ã�x=10��
���Ұ�������Ϊ10+40=50���ˣ����װ�������Ϊ100-50=50���ˣ���
������£�
| ���� | ������ | �ϼ� | |
| �װ� | 20 | 30 | 50 |
| �Ұ� | 10 | 40 | 50 |
| �ϼ� | 30 | 70 | 100 |
| �� | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼���˶����Լ����Ӧ�ã��ηֲ����Լ���ѧ������Ū�����е������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -b+4 | B�� | -b+2 | C�� | b-2 | D�� | b+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 9�� | C�� | $\frac{9��}{2}$ | D�� | $\frac{7��}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
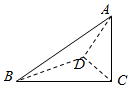 ��֪����A-BCD���ĸ�����A��B��C��D������O�ı����ϣ�AC��ƽ��BCD��BD��AD����AD=2$\sqrt{5}$��BD=2��CD=$\sqrt{3}$������O�����Ϊ��������
��֪����A-BCD���ĸ�����A��B��C��D������O�ı����ϣ�AC��ƽ��BCD��BD��AD����AD=2$\sqrt{5}$��BD=2��CD=$\sqrt{3}$������O�����Ϊ��������| A�� | 8$\sqrt{6}$�� | B�� | $\frac{27\sqrt{3}��}{2}$ | C�� | $\frac{7\sqrt{7}��}{6}$ | D�� | 10$\sqrt{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com