
分析 (1)进行数量积的坐标运算即可;
(2)先求向量$2\overrightarrow{a}-\overrightarrow{b}$和$\overrightarrow{a}+3\overrightarrow{b}$的坐标,然后进行数量积的坐标运算即可;
(3)根据向量夹角余弦的坐标公式进行运算即可;
(4)先写出向量$\overrightarrow{a}+\overrightarrow{b}$和$λ\overrightarrow{b}-\overrightarrow{a}$的坐标,设这两向量夹角为θ,根据cosθ=$\frac{(\overrightarrow{a}+\overrightarrow{b})•(λ\overrightarrow{b}-\overrightarrow{a})}{|\overrightarrow{a}+\overrightarrow{b}||λ\overrightarrow{b}-\overrightarrow{a}|}<0$即可求出λ的取值范围.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}=-15$;
(2)$2\overrightarrow{a}-\overrightarrow{b}=(11,-5),\overrightarrow{a}+3\overrightarrow{b}=(-12,15)$;
∴$(2\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}+3\overrightarrow{b})=-11×12-5×15=-207$;
(3)$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-15}{3×5\sqrt{2}}=-\frac{\sqrt{2}}{2}$;
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为135°;
(4)$\overrightarrow{a}+\overrightarrow{b}=(-2,5)$,$λ\overrightarrow{b}-\overrightarrow{a}=(-5λ-3,5λ)$;
∵$\overrightarrow{a}+\overrightarrow{b}$与$λ\overrightarrow{b}-\overrightarrow{a}$的夹角为钝角,并设该夹角为θ,则:
cosθ=$\frac{35λ+6}{\sqrt{29}•\sqrt{(-5λ-3)^{2}+25{λ}^{2}}}<0$;
∴35λ+6<0;
∴$λ<-\frac{6}{35}$;
∴λ的取值范围为(-∞,-$\frac{6}{35}$).
点评 考查数量积的坐标运算,向量坐标的加法、减法,与数乘运算,向量夹角余弦的坐标公式,向量夹角的概念.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 系数行列式D≠0 | |
| B. | 比例式$\frac{a_1}{a_2}≠\frac{b_1}{b_2}$ | |
| C. | 向量$({\begin{array}{l}{a_1}\\{{a_2}}\end{array}}),({\begin{array}{l}{b_1}\\{{b_2}}\end{array}})$不平行 | |
| D. | 直线a1x+b1y=c1,a2x+b2y=c2不平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | an=3•2n-1-2 | B. | an=3•2n-2 | C. | an=3•4n-1-2 | D. | an=3•2n+1-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
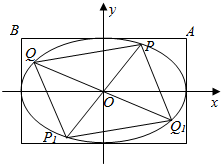 已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4
已知椭圆C的中心在原点,左焦点为F1(-1,0),右准线方程为:x=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
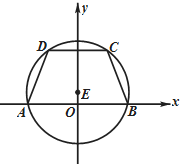 如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.
如图所示,等腰梯形ABCD的底边AB在x轴上,顶点A与顶点B关于原点O对称,且底边AB和CD的长分别为6和2$\sqrt{6}$,高为3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com