
给定椭圆C: (a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为
(a>b>0),称圆C1:x2+y2=a2+b2为椭圆C的“伴随圆”.已知椭圆C的离心率为 ,且经过点(0,1).
,且经过点(0,1).
(1)求实数a,b的值;
(2)若过点P(0,m)(m>0)的直线l与椭圆C有且只有一个公共点,且l被椭圆C的伴随圆C1所截得的弦长为2 ,求实数m的值.
,求实数m的值.
(1)a=2,b=1.(2)m=3.
【解析】
试题分析:(1)利用待定系数法求椭圆方程中参数. 由题意,得b=1,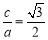 ,c2=a2+b2,解得a=2,b=1.(2)设直线l的方程为y=kx+m,即kx-y+m=0.因为直线l与椭圆C有且只有一个公共点,故方程组
,c2=a2+b2,解得a=2,b=1.(2)设直线l的方程为y=kx+m,即kx-y+m=0.因为直线l与椭圆C有且只有一个公共点,故方程组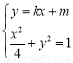 有且只有一组解.从而△=(8km)2-4(1+4k2)( 4m2-4)=0.化简,得m2=1+4k2.①因为直线l被圆x2+y2=5所截得的弦长为2
有且只有一组解.从而△=(8km)2-4(1+4k2)( 4m2-4)=0.化简,得m2=1+4k2.①因为直线l被圆x2+y2=5所截得的弦长为2 ,所以圆心到直线l的距离d=
,所以圆心到直线l的距离d=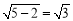 .即
.即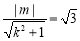 .② 由①②,解得k2=2,m2=9.因为m>0,所以m=3.
.② 由①②,解得k2=2,m2=9.因为m>0,所以m=3.
试题解析:【解析】
(1)记椭圆C的半焦距为c.
由题意,得b=1,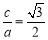 ,c2=a2+b2,
,c2=a2+b2,
解得a=2,b=1. 4分
(2)由(1)知,椭圆C的方程为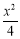 +y2=1,圆C1的方程为x2+y2=5.
+y2=1,圆C1的方程为x2+y2=5.
显然直线l的斜率存在.
设直线l的方程为y=kx+m,即kx-y+m=0. 6分
因为直线l与椭圆C有且只有一个公共点,
故方程组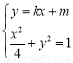 (*) 有且只有一组解.
(*) 有且只有一组解.
由(*)得(1+4k2)x2+8kmx+4m2-4=0.
从而△=(8km)2-4(1+4k2)( 4m2-4)=0.
化简,得m2=1+4k2.① 10分
因为直线l被圆x2+y2=5所截得的弦长为2 ,
,
所以圆心到直线l的距离d=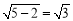 .
.
即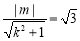 . ② 14分
. ② 14分
由①②,解得k2=2,m2=9.
因为m>0,所以m=3. 16分
考点:直线与椭圆位置关系


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源:2015届江苏省高二第二学期阶段测试文科数学试卷(解析版) 题型:解答题
已知函数 ,
, .
.
(1)若 ,求证:函数
,求证:函数 是
是 上的奇函数;
上的奇函数;
(2)若函数 在区间
在区间 上没有零点,求实数
上没有零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
在平面直角坐标系xOy中,已知直线l的参数方程为 (t为参数 ),圆C的参数方程为
(t为参数 ),圆C的参数方程为 (θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值.
(θ为参数).若点P是圆C上的动点,求点P到直线l的距离的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:填空题
在平面直角坐标系xOy中,已知圆C:x2+y2-6x+5=0,点A,B在圆C上,且AB=2,则 的最大值是 .
的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com