Question

13．已知x，y满足线性规划$\left\{\begin{array}{l}{x+y-4＜0}\\{y-x＞0}\\{2x+y-4＞0}\end{array}\right.$，则x²+y²-6x-4y+14的取值范围是（　　）

• A． [2，14]
• B． （2，14）
• C． [2，$\sqrt{13}$+1]
• D． （2，$\sqrt{13}$+1）

Answer 1

分析 由题意作出其平面区域，（x-3）²+（y-2）²可看成阴影内的点到点C（3，2）的距离的平方，求阴影内的点到C（3，2）的距离的范围可得．

解答 解：由题意作出其平面区域，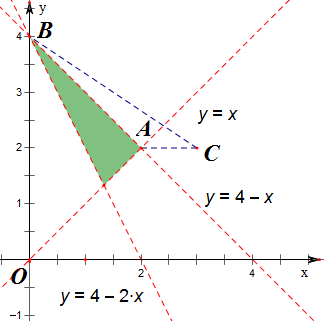

x²+y²-6x-4y+14=（x-3）²+（y-2）²+1，
（x-3）²+（y-2）²可看成阴影内的点到点C（3，2）的距离的平方，又A（2，2），B（0，4）；
故（2-3）²+（2-2）²＜（x-3）²+（y-2）²＜（0-3）²+（4-2）²，
 即1＜（x-3）²+（y-2）²＜13，
故2＜（x-3）²+（y-2）²+1＜14，
故选：B．

点评 本题考查了简单线性规划，作图要细致认真，用到了表达式的几何意义的转化，属于中档题．