
分析 根据双曲线的标准方程可得:a=2,b=$\sqrt{2}$,再由双曲线的定义可得:|AF2|-|AF1|=2a=4,|BF2|-|BF1|=2a=4,所以得到|AF2|+|BF2|-(|AF1|+|BF1|)=8,再根据A、B两点的位置特征可得|AB|是双曲线的通径时,|AB|最小,计算即可得到答案.
解答 解:根据双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$,得a=2,b=$\sqrt{2}$,
由双曲线的定义可得:|AF2|-|AF1|=2a=4…①,
|BF2|-|BF1|=2a=4…②,
①+②可得:|AF2|+|BF2|-(|AF1|+|BF1|)=8,
由于过双曲线的左焦点F1的直线交双曲线的左支于A,B两点,
可得|AF1|+|BF1|=|AB|,当|AB|是双曲线的通径时|AB|最小.
即有|AF2|+|BF2|-(|AF1|+|BF1|)=|AF2|+|BF2|-|AB|=8.
即有|BF2|+|AF2|=|AB|+8≥$\frac{2{b}^{2}}{a}$+8=$\frac{2×2}{2}$+8=10.
故答案为:10.
点评 本题考查两条线段和的最小值的求法,是中档题,解题时要注意双曲线的定义和简单性质的合理运用.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
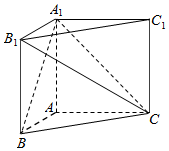 在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.
在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°,设AA1=a.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x±2y=0 | B. | 2x±y=0 | C. | x±y=0 | D. | $\sqrt{2}x±y=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
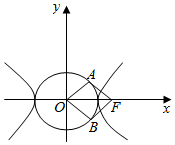 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
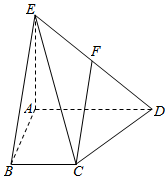 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
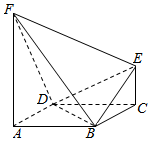 如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.
如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com