
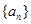 ,
,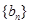 (
(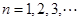 )由下列条件确定:①
)由下列条件确定:①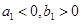 ;②当
;②当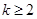 时,
时,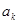 与
与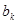 满足:当
满足:当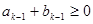 时,
时,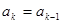 ,
,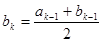 ;当
;当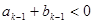 时,
时,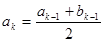 ,
,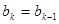 .
.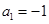 ,
,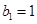 ,写出
,写出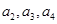 ,并求数列
,并求数列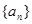 的通项公式;
的通项公式; 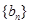 中,若
中,若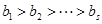 (
(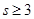 ,且
,且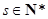 ),试用
),试用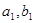 表示
表示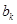
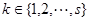 ;
;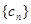
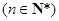 满足
满足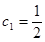 ,
,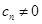 ,
,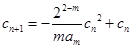 (其中
(其中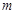 为给定的不小于2的整数),求证:当
为给定的不小于2的整数),求证:当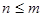 时,恒有
时,恒有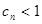 .
.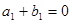 ,所以
,所以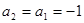 ,
,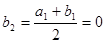 .
.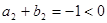 ,所以
,所以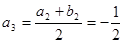 ,
,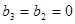 .
.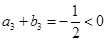 ,所以
,所以 ,
,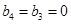 .
.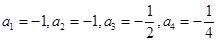 . …………………………………… 2分
. …………………………………… 2分 时,
时,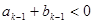 ,则
,则 ,
,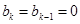 .… 3分
.… 3分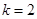 时,已证成立.
时,已证成立. 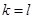 (
(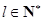 ,且
,且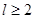 )猜想成立,
)猜想成立,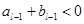 ,
,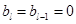 ,
,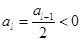 .
.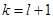 时,由
时,由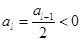 ,
,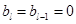 得
得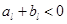 ,则
,则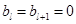 ,
,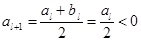 .
.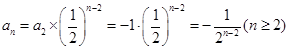 .
.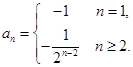 . ……………………………………………… 6分
. ……………………………………………… 6分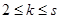 时,假设
时,假设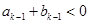 ,根据已知条件则有
,根据已知条件则有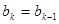 ,
,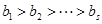 矛盾,因此
矛盾,因此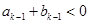 不成立, …………… 7分
不成立, …………… 7分 ,从而有
,从而有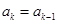 ,所以
,所以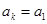 .
. 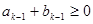 时,
时,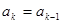 ,
,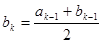 ,
,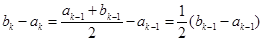 ; …………………… 8分
; …………………… 8分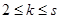 时,总有
时,总有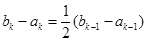 成立.
成立. 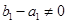 ,
,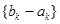 (
(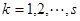 )是首项为
)是首项为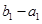 ,公比为
,公比为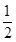 的等比数列,
的等比数列, 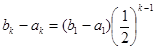 ,
,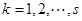 ,
,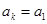 ,所以
,所以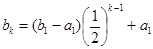 . …………………………… 10分
. …………………………… 10分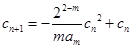
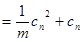 .
.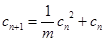 ,所以
,所以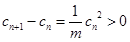 .
.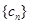 是单调递增数列. …………………………………… 11分
是单调递增数列. …………………………………… 11分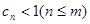 ,只须证
,只须证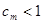 .
.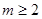 ,则
,则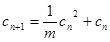 <
<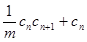 ,即
,即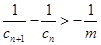 .…… 12分
.…… 12分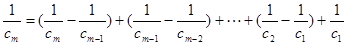
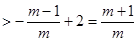 .
.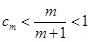 .
.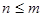 ,恒有
,恒有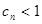 . …………………………………………………14分
. …………………………………………………14分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com