
已知f(x)=xlnx,g(x)=-x2+ax-3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(3)证明对一切x∈(0,+∞),都有lnx>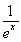 -
-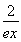 成立.
成立.
(1)f(x)min= (2)a≤4(3)见解析
(2)a≤4(3)见解析
【解析】(1)【解析】
f′(x)=lnx+1,当x∈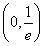 时,f′(x)<0,f(x)单调递减;当x∈
时,f′(x)<0,f(x)单调递减;当x∈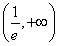 时,f′(x)>0,f(x)单调递增.
时,f′(x)>0,f(x)单调递增.
①当0<t<t+2<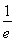 时,t无解;②当0<t<
时,t无解;②当0<t<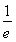 <t+2,即0<t<
<t+2,即0<t<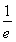 时,f(x)min=f
时,f(x)min=f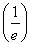 =-
=-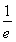 ;
;
③当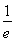 ≤t<t+2,即t≥
≤t<t+2,即t≥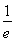 时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,
时,f(x)在[t,t+2]上单调递增,f(x)min=f(t)=tlnt,
所以f(x)min= .
.
(2)【解析】
由题意,要使2xlnx≥-x2+ax-3在x∈(0,+∞)恒成立,即要使a≤2lnx+x+ 恒成立.
恒成立.
设h(x)=2lnx+x+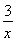 (x>0),则h′(x)=
(x>0),则h′(x)= +1-
+1-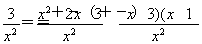 .
.
当x∈(0,1)时,h′(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)单调递增.
所以x=1时,h(x)取得极小值,也就是最小值,
即[h(x)]min=h(1)=4,所以a≤4.
(3)证明:问题等价于证明xlnx>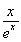 -
-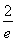 ,x∈(0,+∞).
,x∈(0,+∞).
由(1)知,f(x)=xlnx在(0,+∞)上最小值是-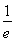 ,
,
当且仅当x=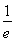 时取得.设m(x)=
时取得.设m(x)=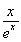 -
-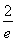 ,x∈(0,+∞),则m′(x)=
,x∈(0,+∞),则m′(x)=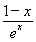 ,
,
易得[m(x)]max=m(1)=-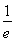 ,
,
当且仅当x=1时取得,
从而对一切x∈(0,+∞),都有lnx>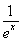 -
-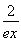 成立
成立


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第4课时练习卷(解析版) 题型:解答题
设函数f(x)是定义在(-1,1)上的偶函数,在(0,1)上是增函数,若f(a-2)-f(4-a2)<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第2课时练习卷(解析版) 题型:填空题
已知函数f(x)=x2-2x,x∈[a,b]的值域为[-1,3],则b-a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第1课时练习卷(解析版) 题型:填空题
下列图象表示函数关系y=f(x)的有________.(填序号)
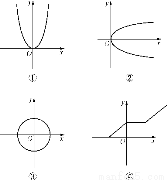
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
设函数f(x)=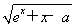 (a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是________.
(a∈R,e为自然对数的底数).若存在b∈[0,1]使f(f(b))=b成立,则a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
已知函数f(x)=||x-1|-1|,若关于x的方程f(x)=m(m∈R)恰有四个互不相等的实根x1,x2,x3,x4,则x1x2x3x4的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:填空题
一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,测得刹车后ts内列车前进的距离为S=27t-0.45t2m,则列车刹车后________s车停下来,期间列车前进了________m.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第13课时练习卷(解析版) 题型:填空题
已知某种产品今年产量为1000件,若计划从明年开始每年的产量比上一年增长10%,则3年后的产量为________件.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第10课时练习卷(解析版) 题型:解答题
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com