
| A. | (-$\sqrt{2}-$1,$\sqrt{2}-1$) | B. | (-$\sqrt{2}-1$,1) | C. | (1,+∞) | D. | (-$\sqrt{2}-1$,$\sqrt{2}-1$)∪(1,+∞) |
分析 利用导数分类求出函数f(x)=a1nx+$\frac{1-a}{2}$x2-x在∈[1,+∞)上的最小值,再由最小值小于$\frac{a}{a-1}$列不等式求得a的取值范围.
解答 解:由f(x)=a1nx+$\frac{1-a}{2}$x2-x,得
f′(x)=$\frac{a}{x}+(1-a)x-1=\frac{(1-a){x}^{2}-x+a}{x}$=$\frac{(x-1)[(1-a)x-a]}{x}$,
当a>1时,f′(x)≤0在[1,+∞)上恒成立,
∴f(x)在[1,+∞)上是减函数,
又当x→+∞时,f(x)→-∞,而$\frac{a}{a-1}$>0,符合题意;
当a≤$\frac{1}{2}$时,f′(x)>0在[1,+∞)上恒成立,
f(x)在[1,+∞)上为增函数,$f(x)_{min}=f(1)=\frac{1-a}{2}-1=-\frac{a+1}{2}$,
由$-\frac{a+1}{2}<\frac{a}{a-1}$,得$-1-\sqrt{2}<a<\sqrt{2}-1$;
当$\frac{1}{2}<a<1$时,f(x)在[1,$\frac{a}{1-a}$)上为减函数,在($\frac{a}{1-a},+∞$)上为增函数,
∴f(x)的最小值为f($\frac{a}{1-a}$)=$aln\frac{a}{1-a}+\frac{1-a}{2}•(\frac{a}{1-a})^{2}-\frac{a}{1-a}$=$a(ln\frac{a}{1-a}+\frac{a-2}{2(1-a)})$,
由$a(ln\frac{a}{1-a}+\frac{a-2}{2(1-a)})<\frac{a}{a-1}$,得$ln\frac{a}{1-a}<\frac{a}{2(a-1)}$,此时显然不成立.
综上,a的取值范围为(-$\sqrt{2}-1$,$\sqrt{2}-1$)∪(1,+∞).
故选:D.
点评 本题考查恒成立问题,考查了利用导数求函数的最值,训练了特称命题的应用,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ln2+1 | B. | ln2-1 | C. | ln3+1 | D. | ln3-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
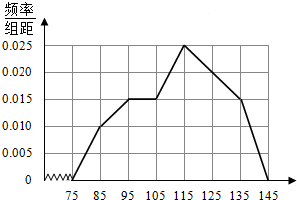 某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )
某同学将全班某次数学考试成绩整理成频率分布直方图后,并将每个小矩形上方线段的中点连接起来得到频率分布折线图(如图所示),据此估计此次考试成绩的众数是( )| A. | 100 | B. | 110 | C. | 115 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com