
| A. | t1和t2有交点(s,t) | B. | t1与t2相交,但交点不一定是(s,t) | ||
| C. | t1与t2必定平行 | D. | t1与t2必定重合 |
分析 由题意知,两个人在试验中发现对变量x的观测数据的平均值都是s,对变量y的观测数据的平均值都是t,所以两组数据的样本中心点是(s,t),回归直线经过样本的中心点,得到直线t1和t2都过(s,t).
解答 解:∵两组数据变量x的观测值的平均值都是s,
对变量y的观测值的平均值都是t,
∴两组数据的样本中心点都是(s,t),
∵数据的样本中心点一定在线性回归直线上,
∴回归直线t1和t2都过点(s,t),
∴两条直线有公共点(s,t).
故选:A.
点评 本题考查回归分析,考查线性回归直线过样本中心点,在一组具有相关关系的变量的数据间,这样的直线可以画出许多条,而其中的一条能最好地反映x与Y之间的关系,这条直线过样本中心点.


科目:高中数学 来源: 题型:选择题
| A. | y=-x | B. | y=-$\frac{1}{2}$x(-$\frac{6}{5}$≤x≤0) | C. | y=-x(-$\frac{4}{5}$≤x≤0) | D. | y=-$\frac{1}{2}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2015f(2015)>e2016f(2016) | B. | e2015f(2015)<e2016f(2016) | ||
| C. | e2015f(2016)>e2016f(2015) | D. | e2015f(2016)<e2016f(2015) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
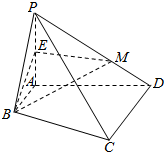 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 0 | 1 | 2 | 3 |
| y | 3 | 3.5 | 4.5 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com