Question

【题目】已知为偶函数．

（1）求实数的值，并写出在区间上的增减性和值域（不需要证明）；

（2）令，其中，若对任意、，总有，求的取值范围；

（3）令，若对任意、，总有，求实数的取值范围．

Answer 1

【答案】（1），在上是增函数，值域为；（2）；（3）.

【解析】

（1）利用偶函数的定义，作差变形可求出，结合函数的解析式写出该函数在区间上的单调性，并利用单调性得出函数在该区间上的值域；

（2）由题意得出，且，换元，构造函数，由可得出二次函数的对称轴，分析函数在区间上的单调性，求出函数的最大值和最小值，结合不等式求出实数的取值范围；

（3）由可得出，求出不等式右边代数式的取值范围，可得出实数的取值范围.

（1）函数为偶函数，则，

即，

由题意知，对任意的，恒成立，则，，

，该函数在区间上为增函数，且，

所以，函数在区间上的值域为；

（2）由题意知，，且，

设，，则，且，

设函数，则，二次函数的对称轴为直线.

，，则函数在区间上单调递增，

则，，

，解得，

，，因此，实数的取值范围是；

（3），

，

，

由，

可得，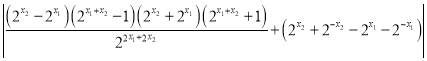

，

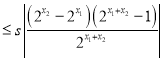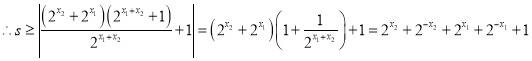由于函数在上单调递增，且，，

，，又，，

所以，，因此，实数的取值范围是.