
已知函数f(x)=alnx+x2 (a为实常数).
(1)当a=﹣4时,求函数f(x)的单调区间;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数;
(3)若 a>0,且对任意的x1,x2∈[1,e],都有|f(x1)﹣f(x2)![]() ,求实数a的取值范围.
,求实数a的取值范围.
考点:
利用导数研究函数的单调性;根的存在性及根的个数判断;导数在最大值、最小值问题中的应用.
专题:
导数的综合应用.
分析:
(1)当a=﹣4时,利用导数的运算法则可得![]() ,在区间(0,+∞)上分别解出f′(x)>0和f′(x)<0即可得出单调区间;
,在区间(0,+∞)上分别解出f′(x)>0和f′(x)<0即可得出单调区间;
(2)当x=1时,方程f(x)=0无解.
当x≠1时,方程f(x)=0(x∈[1,e])等价于方程 ![]() (x∈(1,e]).
(x∈(1,e]).
设g(x)=![]() ,则
,则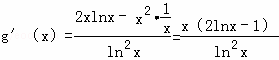 .分别解出g′(x)>0与g′(x)<0即可得出单调性,
.分别解出g′(x)>0与g′(x)<0即可得出单调性,
又g(e)=e2,![]() ,作出y=g(x)与直线y=﹣a的图象,由图象可知a的范围与方程根的关系;
,作出y=g(x)与直线y=﹣a的图象,由图象可知a的范围与方程根的关系;
(3)若a>0时,f(x)在区间[1,e]上是增函数,函数![]() 在区间[1,e]上是减函数.
在区间[1,e]上是减函数.
不妨设1≤x1≤x2≤e,则![]() 等价于
等价于![]() .
.
即![]() ,即函数
,即函数![]() 在x∈[1,e]时是减函数.
在x∈[1,e]时是减函数.
可得![]() ,即
,即![]() 在x∈[1,e]时恒成立.再利用
在x∈[1,e]时恒成立.再利用![]() 在x∈[1,e]时是减函数,即可得出实数a的取值范围.
在x∈[1,e]时是减函数,即可得出实数a的取值范围.
解答:
解:(1)当a=﹣4时,![]() ,
,
当![]() 时,f'(x)<0;当
时,f'(x)<0;当![]() 时,f'(x)>0.
时,f'(x)>0.
∴f(x)的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)当x=1时,方程f(x)=0无解.
当x≠1时,方程f(x)=0(x∈[1,e])等价于方程 ![]() (x∈(1,e]).
(x∈(1,e]).
设g(x)=![]() ,则
,则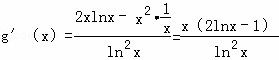 .
.
当![]() 时,g'(x)<0,函数g(x)递减,
时,g'(x)<0,函数g(x)递减,
当![]() 时,g'(x)>0,函数g(x)递增.
时,g'(x)>0,函数g(x)递增.
又g(e)=e2,![]() ,作出y=g(x)与直线y=﹣a的图象,由图象知:
,作出y=g(x)与直线y=﹣a的图象,由图象知:
当2e<﹣a≤e2时,即﹣e2≤a<﹣2e时,方程f(x)=0有2个相异的根;
当a<﹣e2或a=﹣2e时,方程f(x)=0有1个根;
当a>﹣2e时,方程f(x)=0有0个根.
(3)若a>0时,f(x)在区间[1,e]上是增函数,函数![]() 在区间[1,e]上是减函数.
在区间[1,e]上是减函数.
不妨设1≤x1≤x2≤e,
则![]() 等价于
等价于![]() .
.
即![]() ,
,
即函数![]() 在x∈[1,e]时是减函数.
在x∈[1,e]时是减函数.
∴![]() ,即
,即![]() 在x∈[1,e]时恒成立.
在x∈[1,e]时恒成立.
∵![]() 在x∈[1,e]时是减函数,∴
在x∈[1,e]时是减函数,∴![]() .
.
所以,实数a的取值范围是![]() .
.
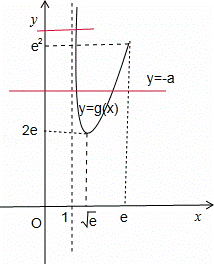
点评:
本题综合考查了利用导数研究函数的单调性、等价转化、适当变形等基础知识与基本技能,考查了数形结合思想方法、推理能力和计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com