练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知z=（1-2i）2+3i+4
    （1）求z及|
    .
    z
    +i    |；
    （2）若
    1+i
    z
    +az+b=2-i求实数a，b的值．
    考点：复数代数形式的乘除运算,复数相等的充要条件,复数求模
    专题：数系的扩充和复数
    分析：（1）利用复数的运算法则即可得出；
    （2）利用复数的运算法则及其复数相等即可得出．
    解答： 解：（1）z=（1-2i）2+3i+4=1-4-4i+3i+4=1-i，
    ∴
    .
    z
    =1+i，
    ∴|
    .
    z
    +i    |=|1+2i|=
    		1+22
    =
    		5
    ；
    （2）
    1+i
    z
    +az+b=2-i即
    1+i
    1-i
    +a(1-i)+b    =2-i，
    ∴
    (1+i)2
    (1-i)(1+i)
    +a+b-2+i-ai=0，
    化为a+b-2+（2-a）i=0，
    ∴
    a+b-2=0
    2-a=0
    ，解得a=2，b=0．
    点评：本题考查了复数的运算法则及其复数相等，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知直线的点斜式方程是y+1=x-2，那么此直线的斜率为（　　）
    A、
    1
    4
    B、
    1
    3
    C、
    1
    2
    D、1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    		3
    2
    sinx-
    1
    2
    cosx，x∈R的最大值为M，最小正周期为T．
    （1）求M、T；
    （2）求函数的单调增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

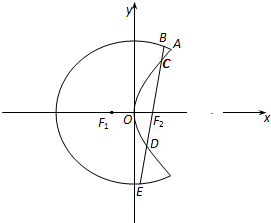    如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．
    （Ⅰ）求曲线C1和C2所在的椭圆和抛物线方程；
    （Ⅱ）过F2作一条与x轴相交的直线l，分别与“月蚀圆”依次交于B、C、D、E四点，
    （1）当直线l⊥x轴时，求
    |CD|
    |BE|
    的值；
    （2）当直线l不垂直x轴时，若G为CD中点、H为BE中点，问
    |CD|•|HF2|
    |BE|•|GF2|
    是否为定值？若是，求出此定值；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    通过随机询问110名性别不同的大学生是否爱好某项运动，其中60名男大学生中有40人爱好此项运动，女大学生中有20人爱好此项运动，其中K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，附表：
    P（k2＞k）0.500.400.250.150.100.050.0250.0100.0050.001
    k0.4550.7081.3232.0722.7063.845.0246.6357.87910.83
    能不能有99%以上的把握认为“爱好该项运动与性别有关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求函数f（x）=x3-3x2在区间[-1，5]上的最值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知a，b，c＞0，求证：S=
    a2
    c+b
    +
    b2
    c+a
    +
    c2
    a+b
    ≥
    1
    2
    （a+b+c）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=4x2-mx+5在区间[-2，+∞）上是增函数．
    （Ⅰ）求实数m的取值范围；
    （Ⅱ）求f（1）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知向量
    a
    =（cosx，-1+sinx），
    b
    =（2cosx，sinx）
    （1）试用sinx表示
    a
    •
    b
    ；
    （2）求
    a
    •
    b
    的最大值及此时的x的值．

    查看答案和解析>>

    同步练习册答案