
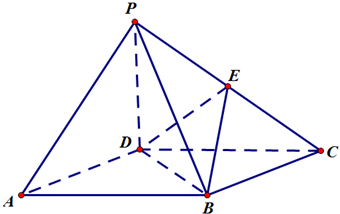
分析 (I)连接AC交BD于O,连接OE,易知O为AC的中点,利用三角形中位线定理、线面平行的判定定理即可得出.
(II)通过建立空间直角坐标系,利用法向量的夹角公式、数量积运算性质即可得出.
(III)对A与C是否同色分类讨论,利用乘法原理与加法原理即可得出.
解答 (I)证明:连接AC交BD于O,连接OE,易知O为AC的中点,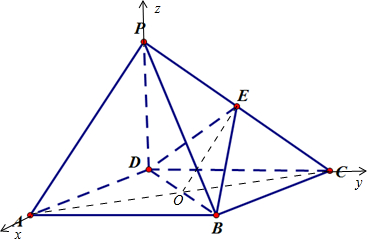
∴OE为△APC的中位线
∴AP∥OE,
又OE?平面BDE,AP?平面BDE,
∴AP∥平面BDE.
(II)解:以DA,DC,DP分别为x,y,z轴建立如图所示的空间直角坐标系.
则A(2,0,0),B(2,2,0),D(0,0,0),E(0,1,1),P(0,0,2),
$\overrightarrow{DE}$=(0,1,1),$\overrightarrow{DB}$=(2,2,0),
设平面BDE的一个法向量$\overrightarrow{n}$=(x,y,z),$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DB}=0}\end{array}\right.$,$\left\{\begin{array}{l}{y+z=0}\\{2x+2y=0}\end{array}\right.$,
$\overrightarrow{n}$=(1,-1,1),又$\overrightarrow{DP}$=(0,0,2).
设二面角A-BD-E的平面角为θ.
则cosθ=-$|cos<\overrightarrow{DP},\overrightarrow{n}>|$=-$\frac{|\overrightarrow{DP}•\overrightarrow{n}|}{|\overrightarrow{DP}||\overrightarrow{n}|}$=-$\frac{2}{2\sqrt{3}}$=-$\frac{\sqrt{3}}{3}$.
∴二面角A-BD-E所成的平面角的余弦值为-$\frac{\sqrt{3}}{3}$.
(III)解:若A与C同色则有5×4×3×1×3=180,
若A与C不同色则有5×4×3×2×2=240.
∴共有180+240=420(种).
点评 本题主要考查立体几何中逻辑推理、空间位置关系、空间角、排列与组合、乘法原理,考查了分类讨论思想、推理能力与计算能力,属于中档题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
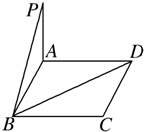 如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB=3,AD=4,PA=1.
如图,P为矩形ABCD所在平面外一点,PA⊥平面ABCD,若已知AB=3,AD=4,PA=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
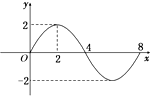 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2 012)的值等于( )| A. | $\sqrt{2}$ | B. | 2+2$\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com