
分析 (1)求得抛物线的焦点坐标和准线方程,运用抛物线的定义可得点$P({\frac{3}{4},m})$在线段OF的中垂线上,可得p=3,进而得到抛物线的方程;
(2)四边形AEBF为菱形.由抛物线的对称性,设点$A({\frac{1}{6}y_0^2,{y_0}})$在x轴的上方,求出抛物线的切线的斜率和切线的方程,令y=0,求得B的坐标,E,F的坐标,由向量相等即可得到四边形的形状.
解答 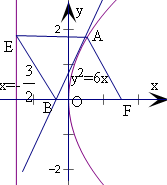 解:(1)抛物线y2=2px(p>0)的焦点F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
解:(1)抛物线y2=2px(p>0)的焦点F($\frac{p}{2}$,0),准线方程为x=-$\frac{p}{2}$,
由题意点$P({\frac{3}{4},m})$到准线的距离为|PO|,
由抛物线的定义,可得点P到准线的距离为|PF|,
即有|PO|=|PF|,即点$P({\frac{3}{4},m})$在线段OF的中垂线上,
则$\frac{p}{4}$=$\frac{3}{4}$,解得p=3,则抛物线的方程为y2=6x;
(2)四边形AEBF为菱形.
证明:抛物线y2=6x的焦点为F($\frac{3}{2}$,0),准线方程为x=-$\frac{3}{2}$,
由抛物线的对称性,设点$A({\frac{1}{6}y_0^2,{y_0}})$在x轴的上方,
由y2=6x,两边对x求导可得,2yy′=6,即y′=$\frac{3}{y}$,
可得点A处的切线的斜率为$\frac{3}{y_0}$,
则点A处切线的方程为$y-{y_0}=\frac{3}{y_0}({x-\frac{1}{6}y_0^2})$,
令上式中y=0,得$x=-\frac{1}{6}y_0^2$,
可得点B的坐标为$({-\frac{1}{6}y_0^2,0})$,又$E({-\frac{3}{2},{y_0}}),F({\frac{3}{2},0})$,
所以$\overrightarrow{FA}=({\frac{1}{6}y_0^2-\frac{3}{2},{y_0}}),\overrightarrow{BE}=({\frac{1}{6}y_0^2-\frac{3}{2},{y_0}})$,
所以$\overrightarrow{FA}=\overrightarrow{BE}$,所以FA∥BE,又AE∥FB,
故四边形AEBF为平行四边形,
再由抛物线的定义,得AF=AE,
所以四边形AEBF为菱形.
点评 本题考查抛物线的定义、方程和性质,注意运用定义法解题,考查直线与抛物线的位置关系:相切,同时考查直线方程的运用,以及化简整理的运算能力,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 金额分组 | [1,5) | [5,9) | [9,13) | [13,17) | [17,21) | [21,25) |
| 频数 | 3 | 9 | 17 | 11 | 8 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
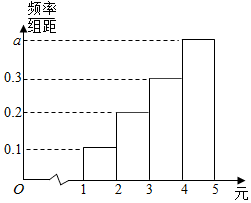 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.
如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 3 | D. | 2或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com