
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
分析 先求出基本事件总数,再求出能两次取出的球颜色不同包含的基本事件个数,由此能求出能两次取出的球颜色不同的概率.
解答 解:∵口袋里装有红球、白球、黑球各1个,这3个球除颜色外完全相同,
有放回的连续抽取2次,每次从中任意地取出1个球,
∴基本事件总数n=${C}_{3}^{1}{C}_{3}^{1}$=9,
能两次取出的球颜色不同包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{1}$=6,
∴能两次取出的球颜色不同的概率p=$\frac{m}{n}$=$\frac{6}{9}$=$\frac{2}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
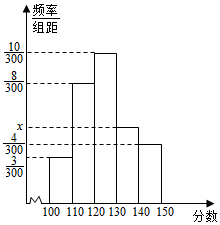 我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.
我市高三某班(共30人)参加永州市第三次模拟考试,该班班主任将全班的数学成绩以[100,109),[110,119),[120,129),[130,139),[140,150)的方式分组,得到频率分布直方图(如图,纵坐标用分数表示),并将分数在120分或者以上的视为优秀.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | 9 | C. | -9 | D. | ±9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com