
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 由条件和正弦定理求出sinA,结合条件和内角的范围求出A,由内角和定理求出B,利用三角形面积公式求出△ABC的面积S.
解答 解:在△ABC中,∵a=$\sqrt{2}$,c=$\sqrt{6}$,C=$\frac{2π}{3}$,
∴由正弦定理得$\frac{a}{sinA}=\frac{c}{sinC}$,
则sinA=$\frac{asinC}{c}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{6}}$=$\frac{1}{2}$,
∵C是钝角,且0<A<π,∴A=$\frac{π}{6}$,
∴B=π-A-C=$\frac{π}{6}$,
∴△ABC的面积S=$\frac{1}{2}acsinB$=$\frac{1}{2}×\sqrt{2}×\sqrt{6}×\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,
故选:D.
点评 本题考查正弦定理,三角形的面积公式的应用,注意内角的范围,属于基础题.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
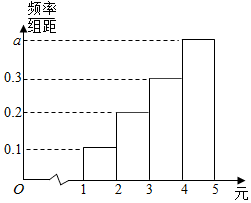 甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.
甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发10个红包,每个红包金额在[1,5]产生.已知在每轮游戏中所产生的10个红包金额的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.
如图,在五面体ABCDE中,AD⊥平面ABC,AD∥BE∥CF,△ABC为等边三角形,AB=2$\sqrt{3}$,BE=2,AD=3,CF=4,M为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{8}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三边均不相等的三角形 | B. | 直角三角形 | ||
| C. | 等腰(非等边)三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 3 | D. | 2或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com