
分析 通过余弦定理分别表示出cosC,cosA和cosB,令其大于0求得x的范围.
解答 解:根据题意知$\left\{\begin{array}{l}{cosC=\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{9+25-{x}^{2}}{30}>0}\\{cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}=\frac{25+{x}^{2}-9}{10x}>0}\\{cosB=\frac{9+{x}^{2}-25}{6x}>0}\end{array}\right.$,
解不等式得4<x<$\sqrt{34}$,
故答案为:(4,$\sqrt{34}$)
点评 本题主要考查了余弦定理的应用.注重了对余弦定理公式灵活运用的考查.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<-$\frac{1}{e}$ | B. | a>-$\frac{1}{e}$ | C. | a<-$\frac{1}{2}$ | D. | a>-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处就没有切线 | |
| B. | 若曲线y=f(x)在点(x0,y0)处有切线,则f′(x0)必存在 | |
| C. | 若f′(x0)不存在,则曲线y=f(x)在点(x0,y0)处的切线斜率不存在 | |
| D. | 若曲线y=f(x)在点(x0,y0)处没有切线,则f′(x0)有可能存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
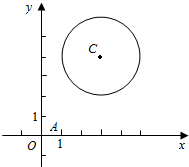 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com